Transforming graphs of functions is something that can be done in Math.
Where we already have the graph of a function, but can apply operations to the function in order to change the location or shape of the graph.
This page will show examples of transformations that can be done to a quadratic graph, and the operations that create them.
The quadratic graph we’ll use is a standard curve shown below, but the transformations shown on this page do also apply to other quadratic graphs that can be encountered.
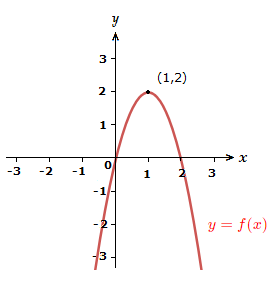
Transforming Graphs of Functions
Examples
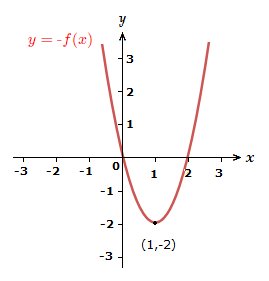
1)
Reflect the graph in the -axis.
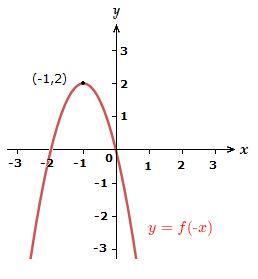
2)
Reflect the graph in the -axis.
3)
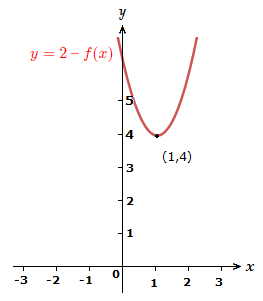
Reflect the graph in the y-axis, then the -axis.
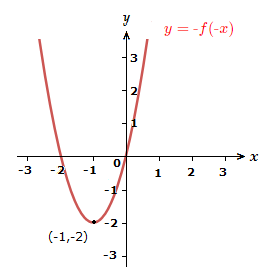
4)
Move the graph up the -axis 1 unit.
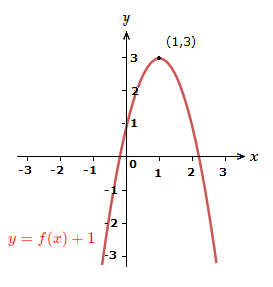
5)
Move the graph along the -axis 1 unit left.
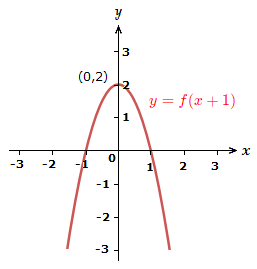
6)
Stretch the graph by 2 in the direction.
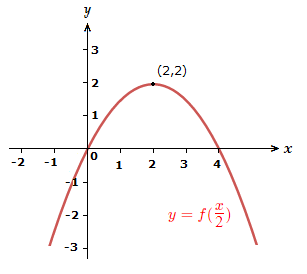
7)
Stretch the graph by 2 in the direction.
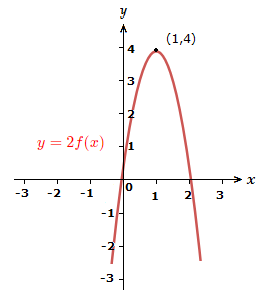
8)
Reflect the graph in the -axis, then move up by 2 units.