Transforming graphs of functions is something that can be done in Math.
Where we already have the graph of a function, but can apply operations to the function in order to change the location or shape of the graph.
This page will show examples of transformations that can be done to a quadratic graph, and the operations that create them.
The quadratic graph we’ll use is a standard curve shown below, but the transformations shown on this page do also apply to other quadratic graphs that can be encountered.
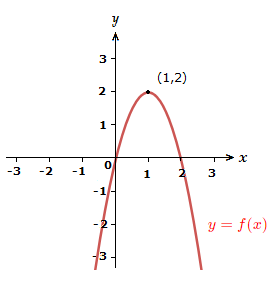
Transforming Graphs of Functions
Examples
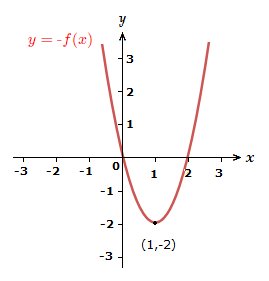
1) y = \space {\text{-}}f(x)
Reflect the graph in the x-axis.
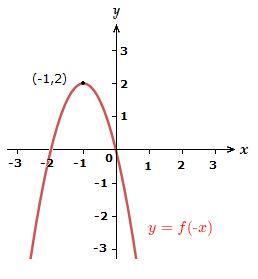
2) y = \space f({\text{-}}x)
Reflect the graph in the y-axis.
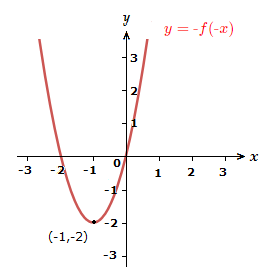
3) y = \space {\text{-}}f({\text{-}}x)
Reflect the graph in the y-axis, then the x-axis.
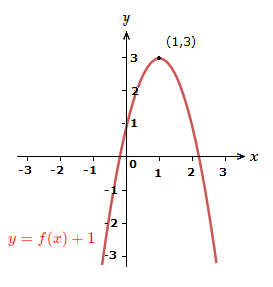
4) y = \space f(x) + 1
Move the graph up the x-axis 1 unit.
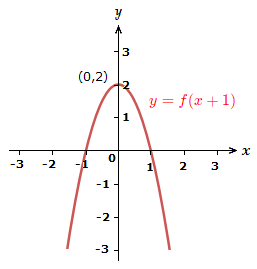
5) y = \space f(x + 1)
Move the graph along the y-axis 1 unit left.
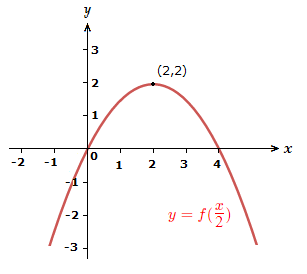
6) y = \space f(\frac{x}{2})
Stretch the graph by 2 in the x direction.
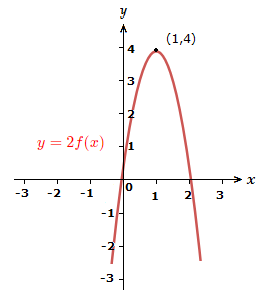
7) y = \space 2f(x)
Stretch the graph by 2 in the y direction.
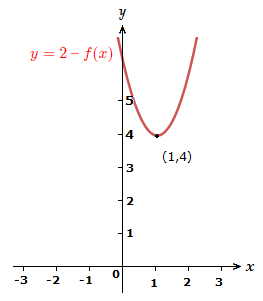
8) y = \space 2 \space {\text{--}} \space f(x)
Reflect the graph in the x-axis, then move up by 2 units.