On the logarithmic and exponential function introduction page, referred to was the natural logarithm function.
The natural logarithm is the following.
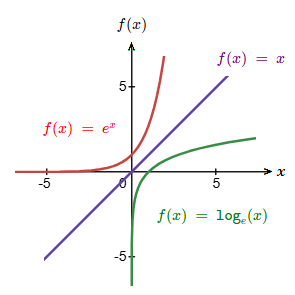
f(x) \space = \space {\tt{log}}_{e} (x)
Sometimes also written as, f(x) \space = \space {\tt{ln}} (x).
Natural Exponential Function
Along with the natural logarithmic function, there is also a natural exponential function.Similar to the standard exponential function. f(x) = a^x
The natural exponential is the following.
f(x) \space = \space e^x
e
The number e is known as Euler’s number.e is as irrational number with no ending point.
e \space = \space 2.718281828459......
The value of e can be calculated or approximated in a few different ways.
One way is with the following series.
e \space = \space\space \displaystyle \sum_{n=0}^{\infin} \space (\space \frac{1}{n!} \space)
We could do n up to 5.
e \space \approx \space\space \displaystyle \sum_{n=0}^{5} \space (\space \frac{1}{n!} \space) \space = \space\space \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!} \space = \space 2.7166...
This page at the intmath.com website shows several ways for calculating e.
Examples
(1.1)
Establish the value of the natural logarithm of 5.172.
Solution
The \tt{ln} button on a calculator can be made use of.
{\tt{ln}}(5.172) \space = \space 1.643
So. e^{1.643} \space \approx \space 5.172
(1.2)
If 120 \space = \space e^t.
What is an approximate value of t
Solution
120 \space = \space e^t ( Can take \tt{ln} of both sides, written as {\tt{log}}_e )
{\tt{log}}_e120 \space = \space {\tt{log}}_ee^t
{\tt{log}}_e120 \space = \space t{\tt{log}}_ee
{\tt{log}}_e120 \space = \space t ( As {\tt{log}}_e e \space = \space 1 )
4.787 \space \approx \space t
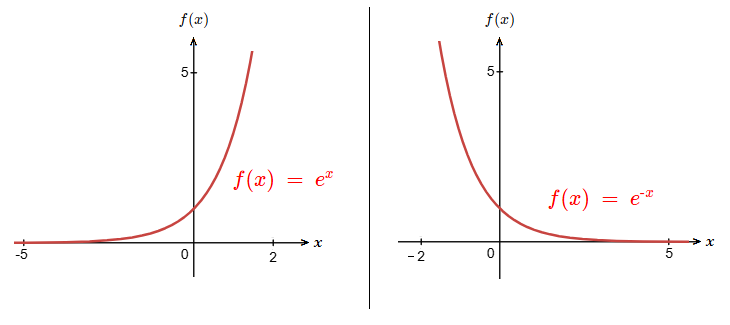
Graph of the Natural Exponential Function
The graph of the natural exponential function is a curve.
The nature of the curve depends on the nature of the value of x.
Inverse of the Natural Exponential
The inverse function of the natural exponential function is the natural logarithm.f(x) \space = \space {\tt{log}}_{e} (x)
As such, their graphs are reflected in the line f(x) = x.