Synthetic Division of Polynomials Examples

Moving on from the box method for division of polynomials, another approach that can be used at times is ‘synthetic division’.

This approach can be used when a polynomial is to be divided by a linear expression with a leading coefficient of  1.  The synthetic division of polynomials examples on this page will show the steps to take in such situations.

Synthetic Division Steps:

We will introduce the first of our synthetic division of polynomials examples by looking at the division of the polynomial   2x^3 + 4x^2 \space {\text{--}} \space 3x \space {\text{--}} \space 3,
by the linear expression   x \space {\text{--}} \space 1.


1)
Sketch half a box, with a left side and a base.

Then write the coefficients and constant of the polynomial along the top of the half box.

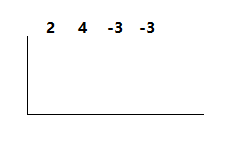
2)
Solve for  x  in the linear expression.

Write this number on the left side of the half box, while also bringing the first coefficient down underneath.

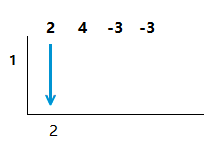
3)
Now multiply this first coefficient underneath by the value we found and placed on the left.

Then place this multiplication result at he base of the next column.

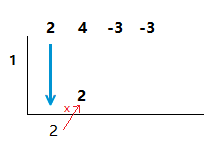
4)
Now add the numbers in this next column together, and place the result underneath the column.

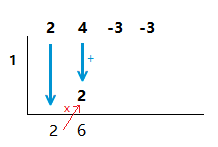
5)
The repeat the same steps for the remaining columns of the half box, until there are no more coefficient columns left to do.

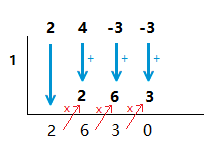
When we are done, the numbers underneath to half box will be the answer to the polynomial division.

The degree of the answer is one less than the dividend, so our answer is   2x^2 + 6x + 3.
When  0  is the final number of the computations involved, there is no remainder to the division sum.

---

Synthetic Division of Polynomials
Examples

(1.1) 

( 2x^3 + 6x^2 + 2x \space {\text{--}} \space 5 ) \space \div \space ( x + 1 )

Solution   

x + 1 = 0 \space \space => \space \space x = {\text{-}}1

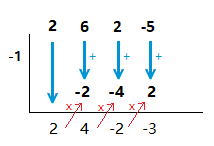
( 2x^3 + 6x^2 + 2x \space {\text{--}} \space 5 ) \space \div \space ( x + 1 ) \space = \space 2x^2 + 4x \space {\text{-}} \space 2 + \frac{3}{x + 1}




(1.2) 

( 3x^3 + 6x^2 \space {\text{--}} \space 3x + 2 ) \space \div \space ( x + 2 )

Solution   

x + 2 = 0 \space \space => \space \space x = {\text{-}}2

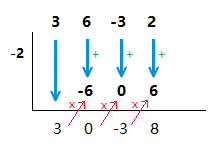
( 3x^3 + 6x^2 \space {\text{--}} \space 3x + 2 ) \space \div \space ( x + 2 ) \space = \space 3x^2 \space {\text{--}} \space 3 + \frac{8}{x + 2}





(1.3) 

( 2x^3 + 5x^2 \space {\text{--}} \space 9x + 4 ) \space \div \space ( 2x \space {\text{--}} \space 1 )

Solution   

Here the leading coefficient of the divisor is not  1,  it is  2.

So we have to make the  2  into a  1  by dividing through by  2.

( 2x \space {\text{--}} \space 1 ) \div 2 \space = \space x \space {\text{--}} \space \frac{1}{2}

x \space {\text{--}} \space \frac{1}{2} = 0 \space \space => \space \space x = \frac{1}{2}

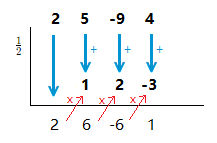
( 2x^3 + 5x^2 \space {\text{--}} \space 9x + 4 ) \space \div \space ( 2x \space {\text{--}} \space 1 ) \space = \space 2x^2 + 6x \space {\text{--}} \space 6 + \frac{1}{2x \space {\text{--}} \space 1}





(1.4) 

( x^3 + 4x + 3 ) \space \div \space ( x + 2 )

Solution   

x + 2 = 0 \space \space => \space \space x = {\text{-}}2

In this example there is no x^2 term in the larger polynomial being divided.
We don’t skip the entry out, instead we place a 0 above, and include it in the synthetic division steps.

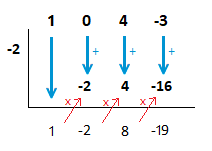
( x^3 + 4x + 3 ) \space \div \space ( x + 2 ) \space = \space x^2 \space {\text{--}} \space 2x + 8 \space {\text{--}} \space \frac{19}{x + 2}





(1.5) 

If   ( x^3 + ax^2 \space {\text{--}} \space 4x + 4 ) \space \div \space ( x \space {\text{--}} \space 1 )   has a remainder of  3.

What is the value of  a?

Solution   

x \space {\text{--}} \space 1 = 0 \space \space => \space \space x = 1

We can proceed by placing a in the correct position above, and following the usual steps.

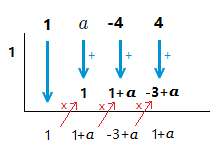
1 + a = 3     =>     1 + a \space {\text{--}} \space 1 = 3 \space {\text{--}} \space 1     =>     a = 2

---

Polynomial Remainder Theorem

Related to synthetic division of polynomials examples is something called the ‘remainder theorem’.


Which is that when a polynomial   f(x)   is divided by   ( x \space {\text{--}} \space h ),
the remainder will be   f(h).


If we remember example (1.2), the remainder was  8,  when dividing by  ( x + 2 ).

So by the remainder theorem, we expect  f({\text{-}}2)  to equal  8.

f(x) \space = \space 3x^3 + 6x^2 \space {\text{--}} \space 3x + 2

f({\text{-}}2) \space = \space 3({\text{-}}2)^3 + 6({\text{-}}2)^2 \space {\text{--}} \space 3({\text{-}}2) + 2

= \space {\text{-}}24 + 24 + 6 + 2 \space = \space 8


This can be a useful way of checking if you have done the correct steps when doing a synthetic division sum.

1. Home
 ›
2. Algebra 1
› Synthetic Division

---

Return to TOP of page