Complex and Imaginary Numbers,
Symbol for Imaginary Numbers

Before learning about complex numbers, it’s key to learn specifically about imaginary numbers first, including the symbol for imaginary numbers.

Complex and imaginary numbers aren’t quite exactly the same thing, but they are best introduced together in Math.

What is an Imaginary Number?

Imaginary numbers appear when we are to deal with the square root of a negative number.

Now normally we think that we can’t have a square root of a negative number, because a number multiplied by itself, either negative or positive, results in a positive number.


For example,   3 × 3  =  9   ,   –3 × –3  =  9   etc.

So    \bf{\sqrt{9}}  =  + 3.


But we don’t seem to be able to find a result for   \bf{\sqrt{{\text{-}}9}}.

This is where imaginary numbers come in.

Symbol for Imaginary Numbers

There is a special number we can use, represented by the letter  i.

Which has the value:   i  =  \bf{\sqrt{{\text{-}}1}}.


This  i  now enables us to find  \bf{\sqrt{{\text{-}}9}}.

\bf{\sqrt{{\text{-}}9}} \space = \space {\sqrt{9 \times {\text{-}}1}} \space = \space {\sqrt{9}}{\sqrt{{\text{-}}1}}   =   \bf{\sqrt{9}}i

\bf{\sqrt{9}}i   =   3i , –3i


General Case:   {\sqrt{{\text{-}}a}}   =   {\sqrt{a}}i

Though sometimes we can write as  i{\sqrt{a}},  which is also perfectly fine as the order doesn’t matter.

Powers of Imaginary Numbers:

Something interesting happens when we raise  i  to a power and multiply it with itself.

i¹  =  i

i²  =  i × i   =   \bf{\sqrt{{\text{-}}1}}\times{\sqrt{{\text{-}}1}}   =   –1

i³  =  –1 × i   =   –i

i⁴  =  –i × i   =   –\bf{\sqrt{{\text{-}}1}}\times{\sqrt{{\text{-}}1}}   =   -( (\bf{\sqrt{{\text{-}}1}}\times{\sqrt{{\text{-}}1}} )   =   -( –1 )   =   1


So we have:

i¹  =  i   ,   i²  =  –1   ,   i³  =  –i   ,   i⁴  =  1.


What’s interesting is that this pattern continues over and over every 4 powers.

So    i⁵  =  i   ,   i⁶  =  –1    ……. and so on.

---

Complex and Imaginary Numbers

Imaginary numbers in Math enable us to create what are known as ‘complex numbers’.

Which are numbers made up of a real part and an imaginary part.

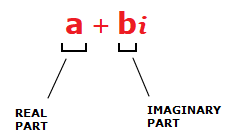
4 + 5i   is an example of a complex number.


But technically, any real number can be thought of as a complex number.

For example if we have the number   4.

This can be thought of as   4 + 0i.

The imaginary part just happens to be 0, which leaves us with just the number  4.

---

Uses and History of Complex Numbers

Complex and imaginary numbers have been around for a few hundred years now.

While at first they did primarily have a use just in Math. In more recent times they have become important in other scientific fields, such as studying electrical currents.


A good article on the history of imaginary numbers can be seen here at the sciencefocus.com website.

While an informative article on some of the applications of complex and imaginary numbers can be viewed here at the issuu website.

1. Home
 ›
2. Algebra 2
› Complex and Imaginary Numbers

---

Return to TOP of page