As seen on the quadratic equations introduction page, quadratic equations have the following general form.
ax^{\tt{2}} + bx + c = 0The factor by grouping page showed examples of how to approach solving quadratics by factoring when possible, this page will show how this approach can be used to solve quadratics by factoring.
Solutions of a Quadratic Equation
Let’s consider a basic example of a quadratic equation. x^{\tt{2}} + x \space {\text{--}} \space 2 = 0
This quadratic equation factors nicely. (x + 2)(x \space {\text{--}} \space 1) = 0
If we set both binomials equal to zero and solve, we obtain two x values.
x + 2 = 0 => x = {\text{-}}2
x \space {\text{--}} \space 1 = 0 => x = 1
Now if we look at the graph of y =x^{\tt{2}} + x \space {\text{--}} \space 2,
we can see what these x values represent.
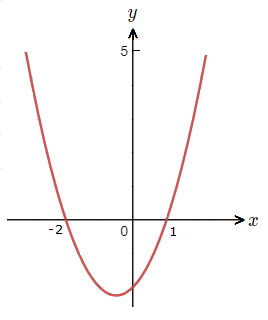
The x values found are the solutions of the quadratic equation. Often also called ‘roots’ or ‘zeroes.
The values with which the graph touches the x-axis.
Usually it’s good practice to input any root values found into the equation to check that they do definitely hold. When solving quadratics by factoring.
({\text{-}}2)^2 + ({\text{-}}2) \space {\text{--}} \space 2 \space = \space 4 \space {\text{--}} \space 2 \space {\text{--}} \space 2 \space = \space 0 ( CORRECT )
(1)^2 + 1 \space {\text{--}} \space 2 \space = 1 + 1 \space {\text{--}} \space 2 \space = \space 0 ( CORRECT )
Solving Quadratics by Factoring Summary:
– With the quadratic equation equal to zero, factor the quadratic expression on the left hand side.– Set the factor terms found equal to zero, and solve them.
– Double check the solutions obtained by inputting into the original quadratic equation.
Solving Quadratics by Factoring Examples
(1.1)
Solve x^{\tt{2}} + 7x \space {\text{--}} \space 8 = 0.
Solution
x^{\tt{2}} + 7x \space {\text{--}} \space 8 = 0
factors to (x \space {\text{--}} \space 1)(x + 8) = 0.
(x \space {\text{--}} \space 1) = 0 => x = 1
(x + 8) = 0 => x = {\text{-}}8
Now to check the found solutions.
x = 1 : 1^{\tt{2}} + 7(1) \space {\text{--}} \space 8 = 1 + 7 \space {\text{--}} \space 8 = 0
x = {\text{-}}8 : ({\text{-}}8)^{\tt{2}} + 7({\text{-}}8) \space {\text{--}} \space 8 = 64 \space {\text{--}} \space 56 \space {\text{--}} \space 8 = 0
(1.2)
Solve 4x^{\tt{2}} + x \space {\text{--}} \space 5 = 0.
Solution
4x^{\tt{2}} + x \space {\text{--}} \space 5 = 0
factors to (4x + 5)(x \space {\text{--}} \space 1) = 0.
(4x + 5) = 0 => x = {\text{-}}{\tt{\frac{5}{4}}}
(x \space {\text{--}} \space 1) = 0 => x = 1
Now to check the found solutions.
x = {\text{-}}{\tt{\frac{5}{4}}} : 4({\text{-}}{\tt{\frac{5}{4}}})^{\tt{2}} + ({\text{-}}{\tt{\frac{5}{4}}}) \space {\text{--}} \space 5 = 4({\tt{\frac{25}{16}}}) \space {\text{--}} \space {\tt{\frac{5}{4}}} \space {\text{--}} \space 5 = 0 = {\tt{\frac{100}{16}}} \space {\text{--}} \space {\tt{\frac{20}{16}}} \space {\text{--}} \space {\tt{\frac{80}{16}}} = 0
x = 1 : 4(1)^{\tt{2}} + 1 \space 5 = 4 + 1 \space {\text{--}} \space 5 = 0
(1.3)
Solve 4x^{\tt{2}} + 12x + 9 = 0.
Solution
4x^{\tt{2}} + 12x + 9 = 0
factors to (2x + 3)(2x + 3) = 0.
(2x + 3) = 0 => x = {\text{-}}{\tt{\frac{3}{2}}}
Two identical roots means there is just one solution overall, which can be called a ‘double root’.
x = {\text{-}}{\tt{\frac{3}{2}}} : 4({\text{-}}{\tt{\frac{3}{2}}})^{\tt{2}} + 12({\text{-}}{\tt{\frac{3}{2}}}) + 9 = 4({\tt{\frac{9}{4}}}) \space {\text{--}} \space {\tt{\frac{36}{2}}} + 9 = {\tt{\frac{36}{4}}} \space {\text{--}} \space {\tt{\frac{72}{4}}} + {\tt{\frac{36}{4}}} = 0