On this Page:
1. Why Solve Quadratic Inequalities
2. How to Solve Quadratic Inequalities
3. Examples
1. Why Solve Quadratic Inequalities
2. How to Solve Quadratic Inequalities
3. Examples
Solving quadratic inequalities follows on from solving linear inequalities, but is a bit more involved and takes a bit more time.
The approach is actually very similar to solving quadratic equations by factoring, but doing a few extra steps.
It helps to first fully understand what we are doing when solving a quadratic inequality, and what exactly the motivation is behind doing so.
Purpose of Solving Quadratic Inequalities
We can observe a standard quadratic graph of the equation, y = x^{\tt{2}} \space {\text{--}} \space x \space {\text{--}} \space 2.
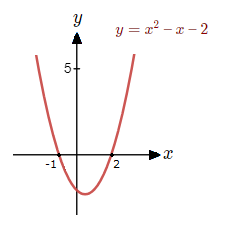
We can see that the graph is below the x-axis between –1 and 2.
If we were to solve the inequality, x^{\tt{2}} \space {\text{--}} \space x \space {\text{--}} \space 2 \space < \space 0[/katex]. We would thus be finding that the graph of the equation is less than zero between the values of -<font size="3">1</font> and <font size="3">2</font>. But how would we go about this? <a name="HowSolveQuadIn"></a> <h3 class="wp-block-heading"><span style="text-decoration: underline;">How to Solve Quadratic Inequalities:</span></h3> There are some clear steps we can follow to solve a quadratic inequality effectively. If we have an inequality of the form, [katex]ax^{\tt{2}} + bx + c \space < \space 0[/katex]. <font size="4"><font color="A30D2B">1)</font></font> Have the inequality in the form where the quadratic is on the other side of the inequality symbol from zero. <font size="4"><font color="A30D2B">2)</font></font> Establish the factors of the quadratic. <font size="4"><font color="A30D2B">3)</font></font> With each factor, set equal to zero and solve. <font size="4"><font color="A30D2B">4)</font></font> Establish the nature of the graph between and outside the values found from solving. <font size="4"><font color="A30D2B">5)</font></font> The solution is the value range that satisfies the original inequality. <b><u><font face="verdana"><font size="4">Ex </font></font></u></b> So if we look at our example above and aim to solve <font size="4">[katex]x^{\tt{2}} \space {\text{--}} \space x \space {\text{--}} 2 < 0[/katex]</font>. We already have the quadratic on the other side from zero. Factoring we get. [katex](x + 1)(x \space {\text{--}} \space 2) < \space 0[/katex] Now solving for equal to zero. [katex]x + 1 = 0 => x = {\text{-}}1 , x \space {\text{--}} \space 2 = 0 => x = 2
At this point, without observing the graph first, we wouldn't know how the quadratic behaves and what the nature is between and outside these values.
We can find this out by plugging a suitable number from each part to find out.
Less than -1, try -2: ({\text{-}}2)^{\tt{2}} \space {\text{--}} \space ({\text{-}}2) \space {\text{--}} \space 2 \space = \space 4 + 2 \space {\text{--}} \space 2 \space = \space 4 ( > 0 )
Between -1 and 2, try 0: (0)^{\tt{2}} \space {\text{--}} \space 0 \space {\text{--}} \space 2 \space = \space {\text{-}}2 ( < 0 )
Greater than 2, try 3: (3)^{\tt{2}} \space {\text{--}} \space 3 \space {\text{--}} \space 2 \space = \space 9 \space {\text{--}} \space 3 \space {\text{--}} \space 2 \space = \space 5 ( > 0 )
So the value range that satisfies the original inequality of being less than zero is between -1 and 2.
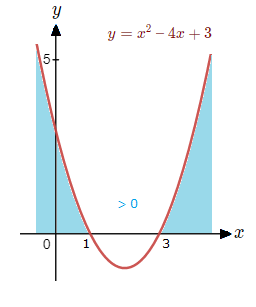
x^{\tt{2}} \space {\text{--}} \space x \space {\text{--}} 2 < \space 0[/katex] for [katex]{\text{-}}1 < x < 2[/katex] <figure class="wp-block-image size-full"><img src="http://www.learnermath.com/wp-content/uploads/2023/09/solving-quadratic-inequalities.png" alt="A graph can sometimes help with understanding solving quadratic inequalities." class="wp-image-871"/></figure> <hr class="wp-block-separator has-alpha-channel-opacity"/> <a name="SolveQuadInEx"></a> <b><font face="times"><font size="5"><font color="30700A"><u>Examples </u></font></font></font></b> <font face="verdana"><font color="3B9446"><u><font size="4"><b><i>(1.1) </i></b></font></u></font></font> Solve <font size="4">[katex]x^{\tt{2}} \space {\text{--}} \space 4x + 3 > 0.
Solution
x^{\tt{2}} \space {\text{--}} \space 4x + 3 > 0
(x \space {\text{--}} \space 1)(x \space {\text{--}} \space 3) > 0
x \space {\text{--}} \space 1 = 0 => x = 1 , x \space {\text{--}} \space 3 = 0 => x = 3
Less than 1, try 0: (0)^{\tt{2}} \space {\text{--}} \space 4(0) + 3 \space = \space 0 + 3 \space = \space 3 ( > 0 )
Between 1 and 3, try 2: (2)^{\tt{2}} \space {\text{--}} \space 4(2) + 3 \space = \space 4 \space {\text{--}} \space 8 + 3 \space = \space {\text{-}}1 ( < 0 )
Greater than 3, try 4: (4)^{\tt{2}} \space {\text{--}} \space 4(4) + 3 \space = \space 16 \space {\text{--}} \space 16 + 3 \space = \space 3 ( > 0 )
The value range that satisfies the original inequality of being greater than zero is less than 1 or larger than 3.
x^{\tt{2}} \space {\text{--}} \space 4x + 3 > \space 0 for x < 1[/katex]</font> or <font size="3">[katex]x > 3
(1.2)
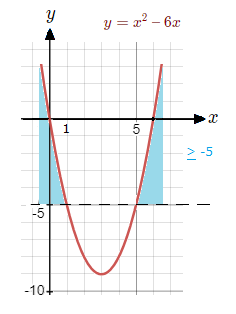
Solve x^{\tt{2}} \space {\text{--}} \space 6x \ge {\text{-}}5.
Solution
For solving quadratic inequalities examples such as this, first alter the form so that the quadratic is on the other side of a zero. Moving 5 across does this.
x^{\tt{2}} \space {\text{--}} \space 6x + 5 \ge 0
(x \space {\text{--}} \space 1)(x \space {\text{--}} \space 5) \ge 0
x \space {\text{--}} \space 1 = 0 => x = 1 , x \space {\text{--}} \space 5 = 0 => x = 5
Less than 1, try 0: (0)^{\tt{2}} \space {\text{--}} \space 6(0) + 5 \space = \space 0 + 5 \space = \space 5 ( > 0 )
Between 1 and 5, try 2: (2)^{\tt{2}} \space {\text{--}} \space 6(2) + 5 \space = \space 4 \space {\text{--}} \space 12 + 5 \space = \space {\text{-}}3 ( < 0 )
Greater than 5, try 6: (6)^{\tt{2}} \space {\text{--}} \space 6(6) + 5 \space = \space 36 \space {\text{--}} \space 36 + 5 \space = \space 5 ( > 0 )
The value range that satisfies the original inequality of being greater than zero is less than 1 or larger than 5.
x^{\tt{2}} \space {\text{--}} \space 6x + 5 \ge 0 for x \le 1 or x \ge 5
These are also the values where x^{\tt{2}} \space {\text{--}} \space 6x \ge {\text{-}}5.
Which we can see in the graph.