It’s possible to establish the area of a regular Pentagon when you have only the apothem line length to work with.
The apothem line in a regular Pentagon is a straight line from the central point of a side, to the central point of the Pentagon itself.
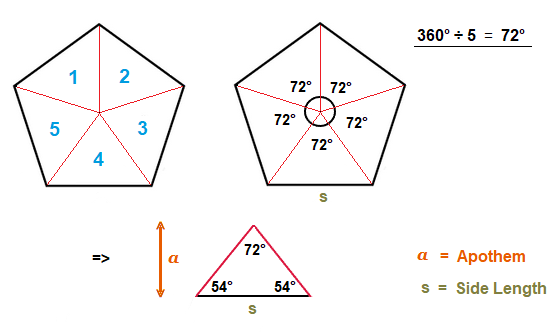
Triangles in a Pentagon
We can split a regular Pentagon up into 5 equal sized triangles.
With each triangle having one inside angle of 72°, and 2 smaller equal sized angles of 54°.
Added to seeing that each triangle base is a side length, and the height is the apothem.
Thus the area of one of the triangles is. \frac{1}{2} × side length × apothem
Splitting the Smaller Triangles:
Now we can split one of these 5 smaller triangles in half into 2 right angle triangles.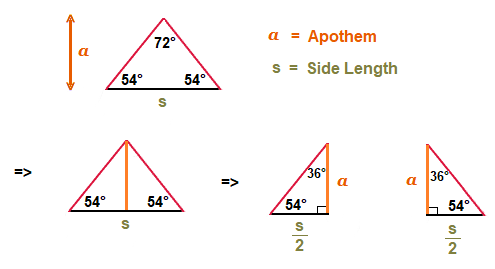
The information from the just one of the right angle triangles can be used to work out a value for the Pentagon side length, when we are initially given only the apothem size.
This means that we can find the area of one of the 5 interior triangles, which then multiplied by 5 gives the whole Pentagon area.
This can be observed in an example below.
Regular Pentagon Area from Apothem Example
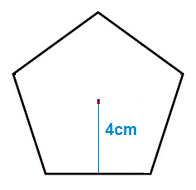
In the case of the Pentagon above, one of the smaller right angle triangles will be the following.
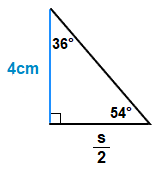
For one of these right angle triangles, we can refer to “SOHCAHTOA” from Trigonometry.
If we focus on the angle 36°, we can write down the tan ratio, opposite side over adjacent side.
From there we can proceed to find a suitable value for s.
tan(36\degree) \space = \space {\Large{\frac{\frac{{\normalsize{s}}}{2}}{\space 4 \space}}} ( × 2 both sides )
2\space tan(36\degree) \space = \space {\Large{\frac{s}{4}}} ( × 4 both sides )
8\space tan(36\degree) \space = \space s , 5.81 \space = \space s
After rounding to 2 decimal places we now have a suitable value for s.
Area of 1 interior triangle = \frac{1}{2} × 5.81 × 4
Area of whole Pentagon = 5 × \frac{1}{2} × 5.81 × 4 = 58.1
The area of the entire regular Pentagon is roughly 58.1cm2.