The factors of polynomials introduction page showed an example of working out the factors of a polynomial of degree 3.
Where we often start out looking for the roots of a polynomial by trying a few initial guesses for values that would give a result of 0 when evaluated in the relevant polynomial.
But to begin with how can we know for sure what values are suitable to try?
This is where we can make use of what is known as the “rational roots theorem” or “rational roots test”.
Rational Roots Theorem
If we have a polynomial a_nx^n \space + \space a_{n \space {\text{–}} \space 1}x^{n \space {\text{–}} \space 1} \space + ….. + \space a_{\tt{2}}x^{\tt{2}} \space \space + a_1x \space + \space a_0 ,
with integer coefficients a_n \space ….. \space a_1,
and a non zero constant term a_0.
Then every rational root of the polynomial is of the form, \color{red}\frac{\pm \space factor \space of \space a_0}{\pm \space factor \space of \space a_n} .
Though we do have to note that not all values obtained with this fraction will be roots/zeros, and sometimes none will be if a polynomial has only complex roots.
In Practice
We can consider a simple quadratic polynomial, f(x) = x^2 + 3x + 2.
This actually factors nicely to (x + 2)(x + 1).
But we’ll still show the rational roots theorem in action.
From the quadratic we can see that, a_n = 1 \space , \space a_0 = 2.
Factors of 1 => 1. Factors of 2 => 1, 2.
\frac{\pm \space 1,2}{\pm \space 1} => ± \frac{1}{1} \space {\tiny{,}} \space \frac{2}{1} => {\scriptsize{\pm}} 1 \space , \space {\scriptsize{\pm}} 2
As we can see, -1 and -2 are among the possible values, which was expected as we knew beforehand that they are the factors.
Evaluating both values should give 0.
f({\text{-}}2) = ({\text{-}}2)^2 + 3({\text{-}}2) + 2 \space = \space 4 \space {\text{–}} \space 6 + 2 \space = \space 0
f({\text{-}}1) = ({\text{-}}1)^2 + 3({\text{-}}1) + 2 \space = \space 1 \space {\text{–}} \space 3 + 2 \space = \space 0
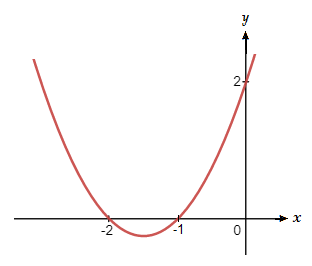
This was a very basic example, it’s when we need to deal with polynomials of degree 3 and larger that using the rational roots theorem is most helpful.
Examples
(1.1)
Find all the possible rational roots of x^4 + 6x^3 + 7x^2 \space {\text{–}} \space 6x \space {\text{–}} \space 8.
Solution
Here, a_n = 1 \space , \space a_0 = {\text{-}}8.
We can just treat the -8 as 8, seeing as we look at plus and minus values of the factors.
Factors of 1 => 1. Factors of 8 => 1, 2, 4, 8.
\frac{\pm \space 1,2,4,8}{\pm \space 1} => ± \frac{1}{1} \space {\tiny{,}} \space \frac{2}{1} \space {\tiny{,}} \space \frac{4}{1} \space {\tiny{,}} \space \frac{8}{1} => {\scriptsize{\pm}} 1 \space , \space {\scriptsize{\pm}} 2 \space , \space {\scriptsize{\pm}} 4\space , \space {\scriptsize{\pm}} 8
(1.2)
Find all the possible rational roots of 2x^3 \space {\text{–}} \space 5x + 6.
Solution
Here, a_n = 2 \space , \space a_0 = 6.
Factors of 2 => 1, 2. Factors of 6 => 1, 2, 3, 6.
\frac{\pm \space 1,2,3,6}{\pm \space 1} => ± \frac{1}{1} \space {\tiny{,}} \space \frac{2}{1} \space {\tiny{,}} \space \frac{3}{1} \space {\tiny{,}} \space \frac{6}{1} => {\scriptsize{\pm}} 1 \space , \space {\scriptsize{\pm}} 2 \space , \space {\scriptsize{\pm}} 3\space , \space {\scriptsize{\pm}} 6
\frac{\pm \space 1,2,3,6}{\pm \space 2} => ± \frac{1}{2} \space {\tiny{,}} \space \frac{2}{2} \space {\tiny{,}} \space \frac{3}{2} \space {\tiny{,}} \space \frac{6}{2} => {\scriptsize{\pm}} {\Large{\frac{1}{2}}} \space , \space {\scriptsize{\pm}} 1 \space , \space {\scriptsize{\pm}} {\Large{\frac{3}{2}}} \space , \space {\scriptsize{\pm}} 3
The possible rational roots are:
{\scriptsize{\pm}} {\Large{\frac{1}{2}}} \space , \space {\scriptsize{\pm}} 1 \space , \space {\scriptsize{\pm}} {\Large{\frac{3}{2}}} \space , \space {\scriptsize{\pm}} 2 \space , \space {\scriptsize{\pm}} 3 \space , \space {\scriptsize{\pm}} 6