Ratio in Statistics Examples,
Ratio Scale, Continued Ratio

The Ratio Introduction page gave an introduction the concept of ratios in Math. With some examples of how they can be simplified from larger numbers in the original ratio similar to how fractions are simplified.

The subject of ratio scale, is where ratios can be appropriately scaled upward or downward where possible, with the use of division and multiplication.
To obtain the information you desire.

A cafe sold slices of cake one week in a ratio of:

Strawberry : Chocolate &nbsp=>&nbsp 1 : 6

If the shop sold &nbsp26&nbsp Strawberry slices that week, how many Chocolate slices were sold?

26  Strawberry slices were sold. &nbsp &nbsp 60 : Chocolate

We know the Chocolate slices sold will be &nbsp6&nbsp times greater,
so some multiplication can complete this ratio being scaled up adequately.

26 × 6 &nbsp=&nbsp 156 &nbsp&nbsp => &nbsp&nbsp 26 : 156

156&nbsp Chocolate cake slices were sold that week.




(1.2)&nbsp

The ratio of spiders to beetles in a garden is &nbsp4 : 1.

If there are &nbsp48&nbsp spiders, how many beetles are there in the garden?

Solution&nbsp &nbsp

We know that &nbsp48&nbsp spiders are in the garden. &nbsp &nbsp 48 : Beetles

The number of beetles in the garden is &nbsp4&nbsp times less, so this situation now calls for division of &nbsp48&nbsp by &nbsp8&nbsp in order to scale the ratio down.

48 ÷ 4 &nbsp=&nbsp 12 &nbsp &nbsp => &nbsp &nbsp 48 : 12

12&nbsp beetles are in the garden.




(1.3)&nbsp

A person works an &nbsp11&nbsp hour shift, and earns &nbsp$154&nbsp for doing so.

How many dollars did the person earn per hour during the &nbsp10&nbsp hour shift?

Solution&nbsp &nbsp

Here we can set up the ratio as, &nbsp Hours : Dollars. &nbsp &nbsp 11 : 154

Now division by &nbsp1&nbsp will scale the ratio down appropriately so that the hours part is just &1.

11 ÷ 11 &nbsp=&nbsp 1 &nbsp &nbsp , &nbsp &nbsp 154 ÷ 11 &nbsp=&nbsp 14 &nbsp &nbsp => &nbsp &nbsp 1 : 14

The person earned &nbsp$20&nbsp per hour during the &nbsp11&nbsp hour shift.

---

Continued Ratio

In Math a ratio can also be in &nbsp3&nbsp parts as well as just &2&nbsp like we’ve seen so far.

When &nbsp3&nbsp or more quantities are presented in a ratio, it is defined as a “continued ratio”.

Meaning that the ratio is continuing beyond &2&nbsp quantities.

Examples &nbsp &nbsp



(2.1)&nbsp

Split &nbsp$20’000&nbsp into the ratio &nbsp 2 : 3 : 5.

Solution&nbsp &nbsp

The ratio &nbsp2 : 3 : 5&nbsp is &nbsp10&nbsp parts in total.

$20’000 ÷ 10 &nbsp=&nbsp $2000

2 × $2000 &nbsp=&nbsp $4000

3 × $2000 &nbsp=&nbsp $6000

5 × $2000 &nbsp=&nbsp $10’000


So &nbsp$20’000&nbsp in the ratio &nbsp2 : 3 : 5 &nbsp=&nbsp $4000 : $6000 : $10’000.





(2.2)&nbsp

A fishing company has &nbsp3&nbsp boats, A, B and C.

One month &nbsp50’000&nbsp fish were caught by the &nbsp3&nbsp boats combined.

The ratio of the fish caught by each mine was,

A : B : C &nbsp&nbsp => &nbsp&nbsp 4 : 2 : 2.

How much fish did each individual boat catch?


Solution&nbsp &nbsp

The ratio of &nbsp 4 : 2 : 2 &nbsp is &nbsp8&nbsp parts in total.

50’000 ÷ 8 &nbsp=&nbsp 6250

BOAT A) &nbsp 4 × 6250 &nbsp=&nbsp25’00

BOAT B) &nbsp 2 × 6250 &nbsp=&nbsp12’500

BOAT C) &nbsp 2 × 6250 &nbsp=&nbsp12’500

The ratio for mines &nbspA, B&nbsp and &nbspC&nbsp is,&nbsp 25’000 : 12’500 : 12’500


Alternatively,&nbsp one can also use the following sums for situations involving ratios such as with the fishing boats above.

Boat’s catch &nbsp = &nbsp Total Amount × \boldsymbol{\frac{Ratio}{Sum \space of \space Ratios}}


So the calculations would be:

BOAT A) &nbsp = &nbsp 50’000 × \bf{\frac{4}{8}} &nbsp = &nbsp 50’000 × \bf{\frac{1}{2}} &nbsp = &nbsp 25’500

BOAT B) &nbsp = &nbsp 50’000 × \bf{\frac{2}{8}} &nbsp = &nbsp 50’000 × \bf{\frac{1}{4}} &nbsp = &nbsp 12’500

BOAT C) &nbsp = &nbsp 50’000 × \bf{\frac{2}{8}} &nbsp = &nbsp 50’000 × \bf{\frac{1}{4}} &nbsp = &nbsp 12’500





(2.3)&nbsp

In certain situations, it can be necessary to be put &nbsp2&nbsp or more ratios into a continued ratio.

Say you had &nbsp3&nbsp different workers at a company that made combined earnings of of &nbsp$46’000&nbsp in one year.


Their combined earnings are divided up between them in ratios such that:

Worker 1 : Worker 2 &nbsp = &nbsp 3 : 4 &nbsp &nbsp &nbsp &nbsp , &nbsp &nbsp &nbsp &nbsp Worker 2 : Worker 3 &nbsp = &nbsp 2 : 1


How much in earnings did each individual worker make?



Solution&nbsp &nbsp

To properly compare these &nbsp3&nbsp different worker earnings, we look to put them into a continued ratio.


In order to do this, we can write out the workers in a &nbsp3&nbsp part ratio along side each other.

Then write down the ratios between the workers that we currently know underneath, set up in the following way.

What we can do now is multiply these numbers in the following way, from the left to the right.

Writing the multiplication results we obtain in order underneath, will give us a continued ratio.

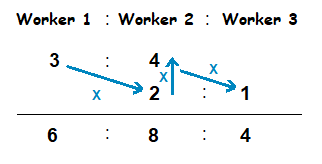
This new ratio we have represents the &nbsp3&nbsp different worker earnings in a continued ratio.

Worker 1 : Worker 2 : Worker 3 &nbsp&nbsp = &nbsp&nbsp 6 : 8 : 4


From here we can take either of the approaches already shown in the fishing boats example &nbsp(2.2).


Sum of Ratios &nbsp=&nbsp 6 + 8 + 4 &nbsp=&nbsp 18

Worker 1) &nbsp = &nbsp 45’000 × \bf{\frac{6}{18}} &nbsp = &nbsp 45’000 × \bf{\frac{1}{3}} &nbsp = &nbsp 15’000

Worker 2) &nbsp = &nbsp 45’000 × \bf{\frac{8}{18}} &nbsp = &nbsp 45’000 × \bf{\frac{4}{9}} &nbsp = &nbsp 20’000

Worker 3) &nbsp = &nbsp 45’000 × \bf{\frac{4}{18}} &nbsp = &nbsp 45’000 × \bf{\frac{2}{9}} &nbsp = &nbsp 10’000

Of the &nbsp$45’000&nbsp total combined earnings.

Worker 1&nbsp made &nbsp$15’000,&nbsp worker 2&nbsp made &nbsp$20’000&nbsp and &nbspworker 3&nbsp made &nbsp$10’000.

1. Home
 ›
2. Probability/Stats
› Ratio, Continued Ratio

---

Return to TOP of page