Along with factoring quadratics, another way to obtain quadratic equation solutions is to use the quadratic formula.
When we have a standard quadratic equation of the form, ax^{\tt{2}} + bx + c = 0.
We can solve this equation with the following “quadratic formula”.
\color{blue}{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}b \space \pm \space \sqrt{b^{2} \space - \space 4ac}}{2a}}}
The presence of a combined plus and minus sign ‘ \pm‘, indicates that there are two possible solutions.
So we can break the quadratic formula down a little bit further.
{\footnotesize{x_1 = \space}} {\boldsymbol{\frac{{\text{-}}b \space + \space \sqrt{b^{2} \space - \space 4ac}}{2a}}} \space \space , \space \space {\footnotesize{x_2 = \space}} {\boldsymbol{\frac{{\text{-}}b \space - \space \sqrt{b^{2} \space - \space 4ac}}{2a}}}
Though sometimes both solutions can be the same value, which means that there is only one solution to the quadratic equation.
Quadratic Formula,
Quadratic Equation Solutions Examples
(1.1)
Solve x^{\tt{2}} + 5x \space {\text{--}} \space 6 = 0.
Solution
This quadratic equation does happen to factor easily to (x+6)(x \space {\text{--}} \space 1).
Giving the solutions x = 1 and x = {\text{-}}6.
But we can see how the quadratic equation solutions are obtained with the quadratic formula also.
Here: a = 1  , b = 5 , c = -6.
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}5 \space \pm \space \sqrt{5^{2} \space - \space (4 \times 1 \times ({\text{-}}6))}}{2 \space \times \space 1}}} {\scriptsize{=}} \space \space {\boldsymbol{\frac{{\text{-}}5 \space \pm \space \sqrt{25 \space + \space 24}}{2}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}5 \space + \space \sqrt{49}}{2}}} , {\boldsymbol{\frac{{\text{-}}5 \space {\text{--}} \space \sqrt{49}}{2}}}
x = 1 or x = {\text{-}}6
(1.2)
Solve 4x^{\tt{2}} + 7x + 2 = 0.
Solution
Here: a = 4 , b = 7 , c = 2.
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}7 \space \pm \space \sqrt{7^{2} \space - \space (4 \times 4 \times 2)}}{2 \space \times \space 4}}} {\scriptsize{=}} \space \space {\boldsymbol{\frac{{\text{-}}7 \space \pm \space \sqrt{49 \space {\text{--}} \space 32}}{8}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}7 \space + \space \sqrt{17}}{8}}} or {\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}7 \space {\text{--}} \space \sqrt{17}}{8}}}
(1.3)
Solve x^{\tt{2}} \space {\text{--}} \space 4x + 4 = 0.
Solution
Here: a = 1 b = -4 , c = 4.
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}({\text{-}}4) \space \pm \space \sqrt{({\text{-}}4)^{2} \space - \space (4 \times 1 \times 4)}}{2 \space \times \space 1}}} {\scriptsize{=}} \space \space {\boldsymbol{\frac{4 \space \pm \space \sqrt{16 \space {\text{--}} \space 16}}{2}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{4 \space + \space 0}{2}}} or {\scriptsize{x = \space}} {\boldsymbol{\frac{4 \space {\text{--}} \space 0}{2}}}
There is only one solution to this quadratic equation solutions example, which is x = 2.
Quadratic Equations,
No Real Solution
It is also possible that there can be no solution or solutions to a quadratic equation in Math.
We can consider the quadratic equation x^{\tt{2}} + 4x + 6 = 0,
and apply the quadratic formula.
a = 1 , b = 4 , c = 6.
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}(4) \space \pm \space \sqrt{(4)^{2} \space - \space (4 \times 1 \times 6)}}{2 \space \times \space 1}}} {\scriptsize{=}} \space \space {\boldsymbol{\frac{{\text{-}}4 \space \pm \space \sqrt{16 \space {\text{--}} \space 24}}{2}}}
{\scriptsize{=}} \space \space {\boldsymbol{\frac{{\text{-}}4 \space \pm \space \sqrt{{\text{-}}8}}{2}}}
Here we have the square root of a negative number, which can be converted to a complex number.
The process of which is shown on the complex numbers page.
It’s the case that \sqrt{{\text{-}}8} can be written as the complex number 2\sqrt{2}i.
So we get:
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}4 \space + \space 2{\sqrt{2}}i}{2}}} or {\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}4 \space {\text{--}} \space 2{\sqrt{2}}i}{2}}}
Which can be simplified a bit further.
x = {\boldsymbol{{\text{-}}2 + {\sqrt{2}}i}} or x = {\boldsymbol{{\text{-}}2 - {\sqrt{2}}i}}
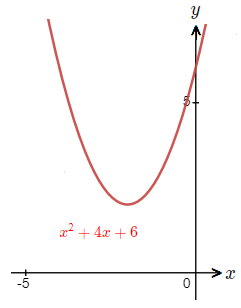
If we look at an image of the graph of x^{\tt{2}} + 4x + 6.
We can see that it does not have any values where it touches the x-axis.
Which is why there are no real solutions to the equation, but instead complex solutions.