As well as being able to establish a regular Pentagon area when knowing only the side length.
We can also do the same when we know only the radius of a regular Pentagon.
Radius of a Pentagon
The radius of a regular Pentagon is a straight line from the central point of the Pentagon, to one of the corners.
As such, there are 5 possible radius lines in a Pentagon.
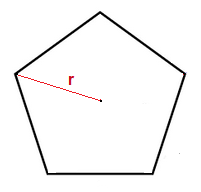
If we think about how the shape of a Pentagon is made up, we can see how to approach finding the area when we know only the value of the radius.
Triangles in a Regular Pentagon, Area
A regular Pentagon can be divided up into 5 equal sized triangles.
This is demonstrated in the image below.
The side lengths of the triangles are the radius lines, and the base is the Pentagon side length s.
The angle opposite the base side s is of size 72°.
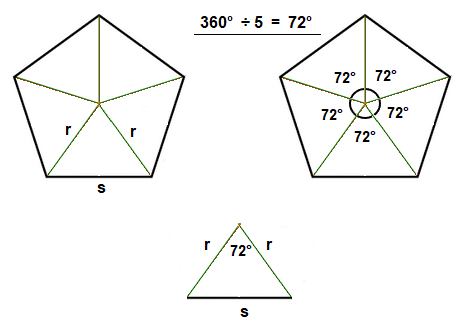
Find Regular Pentagon Area from Radius,
Inner Triangles:
As there are 5 interior triangles, the area of the whole regular Pentagon is the area of one of the interior triangles, multiplied by 5.
For such a triangle, considering the information we have, the area can be calculated in the following way.
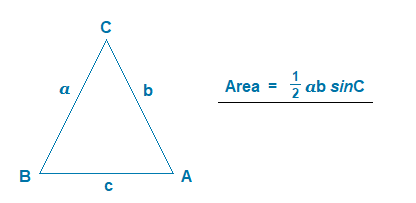
Looking at one of our 5 interior triangles of the regular Pentagon again.
We can see how we can use this formula to work out the whole Pentagon area.
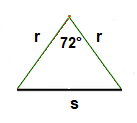
If we apply the same formula to this triangle, we can see how the area can be worked out.
Area = \bf{\frac{1}{2}} × r × r × sin (72°)
= \bf{\frac{1}{2}} × r2 × sin (72°) = \bf{\frac{r^2}{2}} × sin (72°)
Multiplying this result by 5 will give the whole Pentagon area.
5 × \bf{\frac{r^2}{2}} × sin (72°) = \bf{\frac{5r^2}{2}} × sin (72°)
This is the formula that we can use when we wish to find a regular Pentagon area from radius length.
Examples
(1.1)
Find the area of the following regular Pentagon.
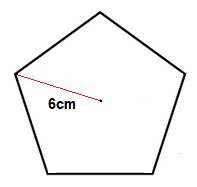
Solution
The radius of the Pentagon is 6cm.
Area = \bf{\frac{5(6)^2}{2}} × sin (72°)
= 90 × sin (72°) = 85.595…
Area of the Pentagon. 85.60cm2 ( to 2 decimal places )
(1.2)
If a regular Pentagon has an area of 80cm2.
Roughly what length is the radius of the Pentagon?
Solution
80 = \bf{\frac{5r^2}{2}} × sin (72°) ( × 2 )
160 = 5r2 × sin (72°) ( ÷ 5 )
32 = r2 × sin (72°) ( ÷ sin(72°) )
\bf{\frac{32}{{\it{sin}}(72\degree)}} = r2
\bf{\sqrt{{\frac{32}{{\it{sin}}(72\degree)}}}} = r , 5.8005… = r
The radius of a regular Pentagon with area 80cm2 is roughly 5.8cm.