Multiplying Decimals Examples

Dealing with multiplying decimals examples can sometimes seem like it may be tough initially, but in truth the process of multiplying decimal numbers is actually simpler than many often expect.

Multiply a Decimal by a Power of 10:

We could have the sum:      0.36 × 100  =  ?

This is quite a simple sum, dealing with multiplication by a power of  10.

The number  100  has  2  zeroes, for us this means that the decimal point will be moving  2  places to the right in  0.36.

Now  36.0  is just  36.

In the same way, if  0.36  was multiplied by  1000:

0.36 × 1000  =  360

Multiplying Decimals Together:

Consider:     0.004 × 0.6  =  ?

A good approach is to initially multiply the numbers in the sum with no decimal points present.

4 × 6  =  24

We can then count how many digits there are after the decimal point in both of the original decimal numbers combined:

0.004 × 0.6
    ^{1 2 3        4}

We can see that there are  4  digits after the point in both numbers together in the original multiplication sum.

So we place a decimal point on the right side of the  24  we worked out, and then move this decimal point  4  places to the left.

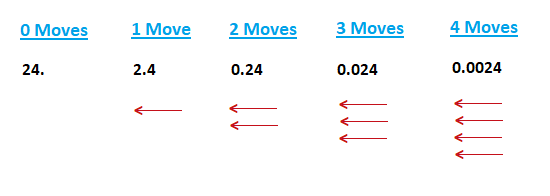
0.004 × 0.6  =  0.0024

---

Multiplying Decimals Examples

(1.1) 

0.3 × 7

Solution   

0.3 × 7
    ¹

There is 1 digit after the decimal point, so the point will move 1 place to the left in the answer.

3 × 7  =  21

21.   ( move 1 place left )   2.1     ,     0.3 × 7 = 2.1




(1.2) 

0.4 × 60

Solution   

0.4 × 60
    ¹

Just 1 digit after the decimal point, so the point will move 1 place left in the answer.

4 × 60  =  240

240.   ( move 1 place left )   24.0

0.4 × 60  =  24.0  =  24




(1.3) 

0.3 × 2.4

Solution   

0.3 × 2.4
    ^{1        2}

Here there are 2 digits beyond the decimal points in the sum.
Thus we move the point 2 places to the left to get the answer.

3 × 24  =  72

72.   ( move 1 place left )   0.72

0.3 × 2.4  =  0.72




(1.4) 

0.06 × 0.07

Solution   

0.06 × 0.07
    ^{1 2        3 4}

Present are 4 digits after the decimal points in the whole sum.
The decimal point will be moved 4 places to the left in the answer.

6 × 7  =  42

42.   ( move 1 place left )   0.0042

0.06 × 0.07  =  0.0042

---

Decimal Long Multiplication Example

(2.1) 

23.4 × 3.2  =  ?

When it comes to multiplying decimals examples where long multiplication is a good option to use.
The same logic also applies, we can multiply like with regular whole numbers, then move the decimal point to the right position in the answer.

Solution   

(step 1)                   (step 2)
\begin{array}{r} \space{\bf{234}}\space\space\\ \times\space\space\space\space\space\space{\bf{2}}\space\space\\ \hline {\bf{468}}\space\space \end{array}             \begin{array}{r} \space{\bf{234}}\space\space\\ \times\space\space\space\space\space\space{\bf{3}}\space\space\space\space\\ \hline {\bf{7020}}\space\space \end{array}


(step 3)

Adding both results:
\begin{array}{r} {\bf{234}}\space\space\\ +\space\space\space\space\space{\bf{7020}}\space\space\\ \hline {\bf{7254}}\space\space \end{array}


23.4 × 3.2
      ^{1       2}
We move the decimal point 2 places to the left.

7254.   =>   72.54

23.4 × 3.2  =  72.54

1. Home
 ›
2. Fractions & Decimals
› Multiplying Decimals

---

Return to TOP of page