A polygon is a flat, two-dimensional (2D) closed shape with straight sides.
Basic examples of such shapes are a triangle, a square or a rectangle.
For regular polygons in particular, there are interior angles of a polygon that follow patterns.
Square or Rectangle
A standard square or rectangle, has 4 right angles contained inside the overall shape.
All of the interior right angles together add up to 360°.
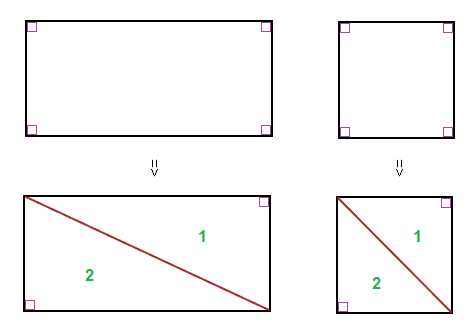
As can be seen, a square or rectangle is composed of 2 smaller right angle triangles.
There are 180° inside a triangle.
It can also be observed that each of the angles inside a square or rectangle shape is the same size, with each angle being 90°.
360° ÷ 4 = 90°Angles in Polygon Shapes
So we have seen the interior angles in and squares and rectangles.
But what about some other shapes, shapes that can have a larger number of sides.
Are the angles that can be found inside some other shapes following a like pattern?
Well, provided the flat 2D shape is a regular polygon, where we have all sides the same length.
Then it’s the case that all interior angles inside will also happen to be the same size as one another.
Like we saw with a square where each inside angle is 90°
There is a handy formula that can help to tell us how many degrees in total there are inside such a regular polygon shape.
Interior Angles of a Polygon:
Polygon Interior Angles Formula
For a regular polygon shape with number of sides n.
The interior angles inside the shape add up to the following total degrees. ( n − 2 ) × 180°.
So the size of one interior angle is given by. \bf{\frac{(n \space {\text{--}} \space 2) \space \times \space 180\degree}{n}}
Examples
(1.1)
Regular pentagon.
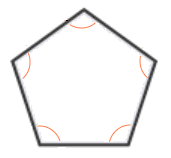
A regular pentagon has 5 straight sides, n = 5
( n − 2 ) × 180°
=> ( 5 − 2 ) × 180°
=> 3 × 180° = 540°
The interior angles of a regular Pentagon sum up to 540°.
Seeing as there are 5 equal angles in the pentagon, we can find the size of each angle.
Interior Angle = \bf{\frac{540\degree}{5}} = 108°
Each individual angle inside a regular Pentagon is 108° in size.
(1.2)
Regular hexagon.
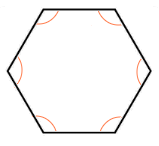
A regular hexagon has 6 straight sides, n = 6
( n − 2 ) × 180°
=> ( 6 − 2 ) × 180°
=> 4 × 180° = 720°
The angles inside a regular Hexagon sum up to a value of 720°.
Interior Angle = \bf{\frac{720\degree}{6}} = 120°Each individual angle inside the Hexagon is 120° in size.
Exterior Angles
Flat 2D polygon shapes in Math, create a certain number of angles with the edges and corners of the shape.
These will be angles that are on the outside of the shape as well as the inside, the outside angles are referred to as exterior angles.
Shapes and Exterior Angles
Different to interior angles, exterior angles are the angles that are formed on the outside of a shape.
An exterior angle is formed between one side of the shape itself, and another straight line that extends from the following side.
Below is a triangle, with the exterior angles drawn in red.
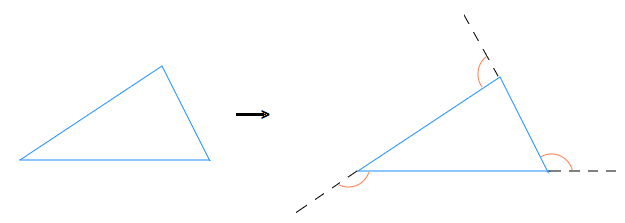
It turns out to be the case that the interior and exterior angle at each point/vertex of a polygon shape sum up to 180°, they are supplementary angles.
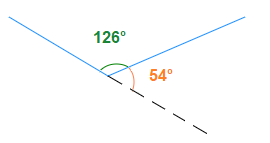
126° + 54° = 180°
Polygons and Exterior Angles
For a regular polygon, that is a polygon where all sides are the same length, and all inside angles the same size, all exterior angles add up to 360°.So for a regular polygon with n number of sides and angles.
To find the value of an exterior angle, you can do the sum:
\frac{360\degree}{n}
Example
(2.1)
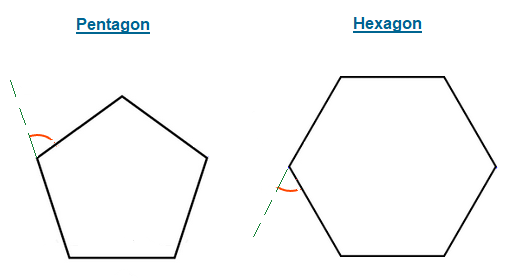
Pentagon External Angle = \tt{\frac{360\degree}{5}} = 72°
Hexagon External Angle = \tt{\frac{360\degree}{6}} = 60°