The inequalities introduction along with the solving inequalities page showed how to write inequalities in basic form, and how to solve inequalities of this sort.
We can also learn how to write inequalities as what are known as “double inequalities”, which is when there are two inequalities symbols present instead of just one.
So in essence we have to inequalities in one, when dealing with a double inequality.
Double Inequalities Form:
Looking at numbers, we can write that 5 is less than 6, and 6 is less than 7 as a double inequality.5 \lt 6 \lt 7
It is a bit neater and easier than writing out two individual inequalities.
5 \lt 6 \space \space , \space \space 6 \lt 7
Just like with individual inequalities, double inequalities can be solved also.
How to Solve Inequalities, Double Inequalities
We could be asked to solve something like, {\text{-}}4 \lt 2x \lt 6.
What we want to do is get the variable x by itself,
like in the case of single inequalities.
This can be done here by dividing through the double inequality by 2, each part needs to have the operation performed.
\frac{{\text{-}}4}{2} \space {\scriptsize{\lt}} \space \frac{2x}{2} \space {\scriptsize{\lt}} \space \frac{6}{2} = {\text{-}}2 \lt x \lt 3
x values less than 3 and greater than 2 are solutions to the inequality.
Examples
(1.1)
Solve 1 \lt x + 3 \lt 5.
Solution
1 \space {\text{--}} \space 3 \space \lt \space x + 3 \space {\text{--}} \space 3 \space \lt \space 5 \space {\text{--}} \space 3
{\text{-}}3 \space {\footnotesize{\lt}} \space x \space {\footnotesize{\lt}} \space 2
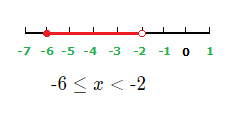
x values less than 2 and greater than –3 are solutions to the inequality.
Graph:
(1.2)
Solve 10 \space {\footnotesize{\le}} \space 4x + 6 \space {\footnotesize{\lt}} \space 18.
Solution
10 \space {\text{--}} \space 6 \space \le \space 4x + 6 \space {\text{--}} \space 6 \space \lt \space 18 \space {\text{--}} \space 6
4 \space \le \space 4x \space \lt \space 12
\frac{4}{4} \space \le \space \frac{4x}{4} \space \lt \space \frac{12}{4}
1 \space \le \space x \space \lt \space 3
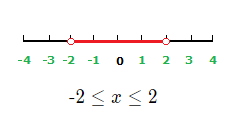
x values less than 3 and greater than or equal to 1 are solutions to the inequality.
Graph:
(1.3)
Solve {\text{-}}3 \space {\footnotesize{\le}} \space 5 \space {\text{--}} \space 2x \space {\footnotesize{\lt}} \space 11.
Solution
{\text{-}}3 \space {\text{--}} \space 5 \space {\footnotesize{\le}} \space 5 \space {\text{--}} \space 2x \space {\text{--}} \space 5 \space {\footnotesize{\lt}} \space 11 \space {\text{--}} \space 5
{\text{-}}8 \space {\footnotesize{\le}} \space {\text{-}}2x \space {\footnotesize{\lt}} \space 6
\frac{{\text{-}}8}{{\text{-}}2} \space \le \space \frac{{\text{-}}2x}{{\text{-}}2} \space \lt \space \frac{6}{{\text{-}}2}
Dividing by a negative number flips the inequality signs.
4 \space \ge \space x \space \gt \space {\text{-}}3
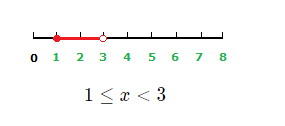
x values less than or equal to 4 and greater than –3 are solutions to the inequality.
Graph:
(1.4)
Solve 4 \space {\footnotesize{\lt}} \space 2 \space {\text{--}} \space a \space {\footnotesize{\le}} \space 8.
Solution
4 \space {\text{--}} \space 2 \space {\footnotesize{\lt}} \space 2 \space {\text{--}} \space x \space {\text{--}} \space 2 \space {\footnotesize{\lt}} \space 8 \space {\text{--}} \space 2
2 \space \lt \space {\text{-}}x \space \le \space 6
2 {\footnotesize{\times}} ({\text{-}}1) \space \lt \space {\text{-}}x {\footnotesize{\times}} ({\text{-}}1) \space \le \space 6 {\footnotesize{\times}} ({\text{-}}1)
Like division, multiplying by a negative number flips the inequality signs.
{\text{-}}2 \space \gt \space x \space \ge \space {\text{-}}6
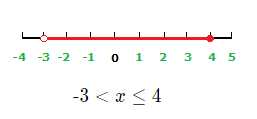
x values less than –2 and greater than or equal to –6 are solutions to the inequality.
Graph: