The completing the square page showed how to approach solving quadratic equations with the complete the square method.
This method can also be used when learning how to graph quadratics, when we want to sketch the appropriate curve.
When solving by completing the square we converted a standard quadratic equation, ax^{\tt{2}} + bx + c = 0,
into the form: a(x + k)^{\tt{2}} = h.
How to Graph Quadratics with
Complete the Square
With graphing using the complete the square method, we convert a quadratic of the form y = ax^{\tt{2}} + bx + c = 0,
to the form: y = a(x + k)^{\tt{2}} + h.
Which is known as the vertex form of a quadratic.
Now when attempting to graph a quadratic curve, we generally want to know the following information.
– Coordinates of the maximum or minimum turning point.
– Any points on the curve that touch the x or y axis.
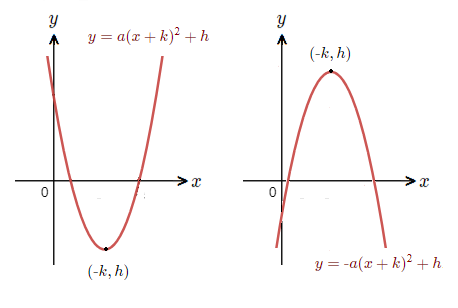
The vertex form assists with working out how to graph quadratics because if a is positive, the curve will have a minimum turning point.
If a is negative, the curve will have a maximum turning point.
Along with the coordinates of the turning point being ({\text{-}}k , h).
It’s best to see this process in action in some examples below of how to graph quadratics.
Examples
(1.1)
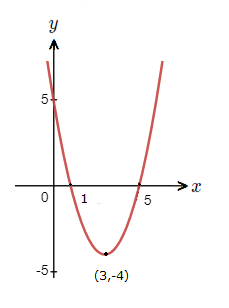
Sketch the graph of y = x^{\tt{2}} \space {\text{--}} \space 6x + 5 with completing the square.
Solution
So we first want to write the original quadratic in vertex form.
x coefficient is 6. \frac{6}{2} = 3 \space , \space 3^2 = 9
y = \space x^{\tt{2}} \space {\text{--}} \space 6x + 9 + 5 \space {\text{--}} \space 9
y = \space x^{\tt{2}} \space {\text{--}} \space 6x + 3 \space {\text{--}} \space 4 => y = (x \space {\text{--}} \space 3)^{\tt{2}} \space {\text{--}} \space 4
The quadratic curve has a minimum turning point at (3 , {\text{-}}4).
The curve will touch the x-axis when y = 0.
(x \space {\text{--}} \space 3)^{\tt{2}} \space {\text{--}} \space 4 = 0 when (x \space {\text{--}} \space 3) = \pm 2.
At x = 5 \space , \space x = 1.
The curve will touch the y-axis when x = 0.
(0 \space {\text{--}} \space 3)^{\tt{2}} \space {\text{--}} \space 4 \space = \space 9 \space {\text{--}} \space 4 \space = \space 5
(1.2)
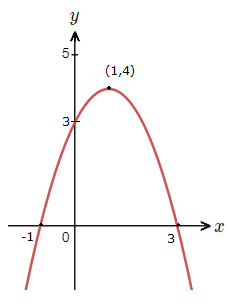
Sketch the graph of y = {\text{-}}x^{\tt{2}} + 2x + 3 with completing the square.
Solution
Here firstly the x^{\tt{2}} coefficient is -1, but to proceed with completing the square we need it to be positive.
So we do the necessary multiplication first.
({\text{-}}x^{\tt{2}} + 2x + 3) \times {\text{-}}1 \space \space = \space \space x^{\tt{2}} \space {\text{--}} \space 2x \space {\text{--}} \space 3
x coefficient is {\text{-}}2. \frac{{\text{-}}2}{2} = {\text{-}}1 \space , \space ({\text{-}}1)^2 = 1
y = \space x^{\tt{2}} \space {\text{--}} \space 2x + 1 \space {\text{--}} \space 3 \space {\text{--}} \space 1
y = \space x^{\tt{2}} \space {\text{--}} \space 2x + 1 \space {\text{--}} \space 4 => y = (x \space {\text{--}} \space 1)^{\tt{2}} \space {\text{--}} \space 4
But to get the proper vertex form, we need to redo the multiplication from the beginning, to get a back to being negative.
(x \space {\text{--}} \space 1)^{\tt{2}} \space {\text{--}} \space 4 \times {\text{-}}1 \space = \space {\text{-}}(x \space {\text{--}} \space 1)^{\tt{2}} + 4
y = {\text{-}}(x \space {\text{--}} \space 1)^{\tt{2}} + 4
The quadratic curve has a maximum turning point at (1 , 4).
The curve will touch the x-axis when y = 0.
{\text{-}}(x \space {\text{--}} \space 1)^{\tt{2}} + 4 = 0 when (x \space {\text{--}} \space 1) = \pm 2.
At x = 3 \space , \space x = {\text{-}}1.
The curve will touch the y-axis when x = 0.
{\text{-}}(0 \space {\text{--}} \space 1)^{\tt{2}} + 4 \space = \space {\text{-}}1 + 4 \space = \space 3