The sizes of angles can be measured in degrees, but with what’s known as radian measure we can also measure angles in radians.
The main initial difference between the two values at first is that a radian is larger in size than a degree.
However they both do the same relevant task, which is to measure an angle size.
Further in the page will see how to find radian measure when we already know an angle size in degrees.
It’s a fairly similar situation to how both Fahrenheit and Celsius can be used to measure a certain temperature.
Despite the scales differing slightly, they are both still reasonable and fine measurements to use.
But sometimes in some instances, one measurement can be more appropriate to use than the other, and this also happens to be the case with radians and degrees at times.
Radian Size
With radians, 1 radian is roughly equal to 57.2958….. degrees.
So 1 radian is slightly larger than 57 times larger than 1 degree.
One whole radian also has an arc length on the outer edge of a circle, which happens to be the same length as the radius of the circle r.
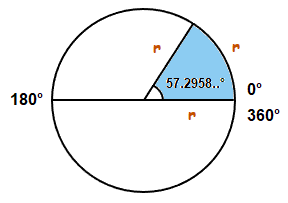
There are 2π radians in a full circle, and π radians in a half circle.
π = 3.14… , π radians = 3.14… radians2π = 6.28… , 2π radians = 6.28… radians
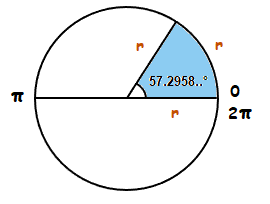
So the following can be understood.
\boldsymbol{\frac{\pi}{2}} radians = 90° , π radians = 180° and 2π radians = 360°.
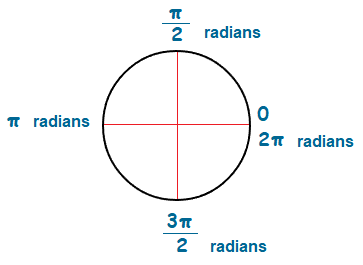
Degrees can often be easier to work with than radians.
But there can be times where it‘s more appropriate to use radian measure instead of degrees. Particularly in Trigonometry and Calculus.
Thus it is important to know how to switch between the two measurements and be comfortable doing so.
Below are some examples of how to convert degrees to radians, and radians to degrees.
Degrees to Radians,
How to Find Radian Measure
If we have an angle θ°, then the degree size of the angle can be converted to radians in the following way:
For θ°. RADIANS = \bf{\frac{\boldsymbol{\theta}}{180}} × πExamples
(1.1)
Convert 60° to radians.
Solution
RADIANS = \bf{\frac{60}{180}} = \bf{\frac{1}{3}} × π = \bf{\frac{\boldsymbol{\pi}}{3}}
60° = \bf{\frac{\boldsymbol{\pi}}{3}} Radians
(1.2)
Convert 3000° to Radians:
Solution
RADIANS = \bf{\frac{300}{180}} = \bf{\frac{5}{3}} × π = \bf{\frac{5\boldsymbol{\pi}}{3}}
300° = \bf{\frac{5\boldsymbol{\pi}}{3}} Radians
(1.3)
Convert 146° to Radians.
Solution
Sometime the fractions for a radian value aren’t given quite so cleanly, and we get a number instead.
When this is the case, we can use decimal form and perform multiplication with the numerical value of π.
The process of how to find radian measure though is still the same.
146° = 2.548 Radians
NOTE
2.48 radians isn’t the same value as 2.48π radians.
In the same way that \bf{\frac{3\boldsymbol{\pi}}{2}} radians isn’t the same as \bf{\frac{3}{2}} radians.
Because \bf{\frac{3}{2}} radians is just that, \bf{\frac{3}{2}} radians. Or 1.5 radians in decimal form.
However \bf{\frac{3\boldsymbol{\pi}}{2}} radians, is a larger value.
\bf{\frac{3 \space \times \space \boldsymbol{\pi}}{2}} = 4.71.
So
\bf{\frac{3\boldsymbol{\pi}}{2}} radians is 4.71 radians.
This is a difference that is important to remember.
Convert Radians to Degrees
Converting in the other direction, radian measure can be converted to degrees by using the following formula.
DEGREES = \bf{\frac{a\boldsymbol{\pi}}{b}} × \bf{\frac{180\degree}{\boldsymbol{\pi}}}Examples
(2.1)
Convert \bf{\frac{3\boldsymbol{\pi}}{4}} radians to degrees.
SolutionDEGREES:
\bf{\frac{3\boldsymbol{\pi}}{4}} × \bf{\frac{180\degree}{\boldsymbol{\pi}}} = \bf{\frac{3 \space \times \space 180\degree}{4}} = \bf{\frac{540\degree}{4}} = 135°
\bf{\frac{3\boldsymbol{\pi}}{4}} Radians = 135°
(2.2)
Convert 1.4 radians to degrees.
Solution
Like with the case of degrees, there are times when we can be given slightly less exact values to convert.
But the approach that we use still works in the same way.
1.4 × \bf{\frac{180\degree}{\boldsymbol{\pi}}} = \bf{\frac{1.4 \space \times \space 180\degree}{\boldsymbol{\pi}}} = 80.21°
1.4 Radians = 80.21°
Radians and Degrees Table
The table below shows some common conversions between degrees and radians.
