A common and effective approach to solving polynomials that we have focused on a lot thus far is using synthetic division.
This page will look at further examples of factoring with synthetic division and solving with polynomials of degree 3 and higher.
Factoring with Synthetic Division and Solving,
Examples
(1.1)
Show that (x + 1) is a factor of f(x) = 3x^3 \space {\text{–}} \space 7x^2 \space {\text{–}} \space 18x \space {\text{–}} \space 8,
then factorise fully and solve for f(x) = 0.
Solution
x + 1 \space = \space 0 \space => \space x = {\text{-}}1
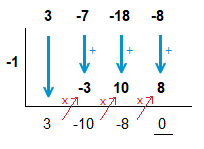
A remainder of 0 shows that (x + 1) is a factor,
and we can now factorise fully and solve.
(3x^2 \space {\text{–}} \space 10x \space {\text{–}} \space 8)(x + 1)
The larger quadratic turns out to factorise nicely into two neat binomials.
(3x \space {\text{–}} \space \space \space \space )(x \space {\text{–}} \space \space \space \space )(x + 1) => (3x + 2)(x \space {\text{–}} \space 4)(x + 1)
Setting the factors equal to 0 and solving will give us the solutions.
3x + 2 = 0 \space \space {\scriptsize{=>}} \space \space x = {\text{-}}\frac{2}{3} \space \space \space , \space \space \space x \space {\text{–}} \space 4 = 0 \space \space {\scriptsize{=>}} \space \space x = 4
x + 1 = 0 \space \space {\scriptsize{=>}} \space \space x = {\text{-}}1
The solutions of 3x^3 \space {\text{–}} \space 7x^2 \space {\text{–}} \space 18x \space {\text{–}} \space 8 are x = {\text{-}}1 \space , \space {\text{-}}\frac{2}{3} \space , \space 4.
(1.2)
If (x \space {\text{–}} \space 2) is a factor of f(x) = x^3 + 3x^2 \space {\text{–}} \space 4x \space {\text{–}} \space 12.
Use synthetic division to find the other two factors, and subsequently all roots.
Solution
We’re given the information that (x {\text{–}} \space 2) is a factor, so can procced straight away with synthetic division without having to make any guesses at values to try.
x \space {\text{–}} \space 2 \space = \space 0 \space => \space x = 2
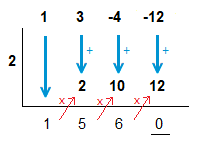
A remainder of 0 is obtained as expected,
and we can now factorise fully and find the roots/solutions.
(x^2 + 5x + 6)(x \space {\text{–}} \space 2)
The larger quadratic turns out to factorise nicely into two neat binomials.
(x \space {\text{–}} \space \space \space \space )(x \space {\text{–}} \space \space \space \space )(x \space {\text{–}} \space 2) => (x + 3)(x + 2)(x \space {\text{–}} \space 2)
Setting the factors equal to 0 and solving will give us the solutions.
x + 3 = 0 \space \space {\scriptsize{=>}} \space \space x = {\text{-}}3 \space \space \space , \space \space \space x \space {\text{–}} \space 2 = 0 \space \space {\scriptsize{=>}} \space \space x = 2
x + 2 = 0 \space \space {\scriptsize{=>}} \space \space x = {\text{-}}2
The solutions of f(x) = x^3 + 3x^2 \space {\text{–}} \space 4x \space {\text{–}} \space 12 are x = {\text{-}}3 \space , \space {\text{-}}2 \space , \space 2.
(1.3)
Find the roots/zeros of h(x) = x^3 \space {\text{–}} \space 3x^2 \space {\text{–}} \space 10x + 24.
Solution
Sometimes we aren’t given any factors or roots to start with.
We can apply the rational roots test, but we can also just proceed with a few basic initial guesses to find a first factor and root.
h(1) = 1^3 \space {\text{–}} \space 3(1)^2 \space {\text{–}} \space 10(1) + 24 \space = \space 1 \space {\text{–}} \space 3 \space {\text{–}} \space 10 + 24 \space = \space 13
h({\text{-}}1) = ({\text{-}}1)^3 \space {\text{–}} \space 3({\text{-}}1)^2 \space {\text{–}} \space 10({\text{-}}1) + 24 \space = \space {\text{-}}1 \space {\text{–}} \space 3 + 10 + 24 \space = \space 13
h(2) = 2^3 \space {\text{–}} \space 3(2)^2 \space {\text{–}} \space 10(2) + 24 \space = \space 8 \space {\text{–}} \space 12 \space {\text{–}} \space 20 + 24 \space = \space 0
2 is a root, so with that information we can proceed with finding the other roots.
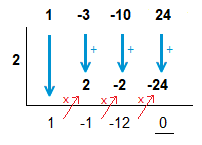
A remainder of 0 is obtained as expected,
and we can now factorise fully and find the roots/solutions.
(x^2 \space {\text{–}} \space x \space {\text{–}} \space 12)(x \space {\text{–}} \space 2)
(x \space {\text{–}} \space \space \space \space )(x \space {\text{–}} \space \space \space \space )(x \space {\text{–}} \space 2) => (x + 3)(x \space {\text{–}} \space 4)(x \space {\text{–}} \space 2)
x + 3 = 0 \space \space {\scriptsize{=>}} \space \space x = {\text{-}}3 \space \space \space , \space \space \space x \space {\text{–}} \space 4 = 0 \space \space {\scriptsize{=>}} \space \space x = 4
The solutions of h(x) = x^3 \space {\text{–}} \space 3x^2 \space {\text{–}} \space 10x + 24 are x = {\text{-}}3 \space , \space 2 \space , \space 4.
(1.4)
Show that (x + 2) is a factor of f(x) = x^4 + 8x^3 + 17x^2 \space {\text{–}} \space 2x \space {\text{–}} \space 24.
Hence factorise fully and solve.
Solution
f(x) here is a polynomial of degree 4, so there are 4 factors and solutions.
Firstly we deal with showing that (x + 2) is a factor.
f({\text{-}}2) = ({\text{-}}2)^4 + 8({\text{-}}2)^3 + 17({\text{-}}2)^2 \space {\text{–}} \space 2({\text{-}}2) \space {\text{–}} \space 24
= 16 \space {\text{–}} \space 64 + 68 + 4 \space {\text{–}} \space 24 \space = \space 0
(x + 2) is a factor, with -2 being a zero.
With that information we can proceed with finding the other roots.
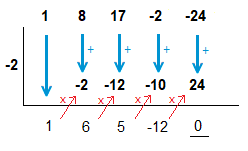
A remainder of 0 is obtained as expected,
we can now look to factorise further.
(x + 2)(x^3 + 6x^2 + 5 \space {\text{–}} \space 12)
We can proceed with factoring with synthetic division for x^3 + 6x^2 + 5 \space {\text{–}} \space 12, but we don’t know any exact zeros/roots to start with.
The rational roots theorem can help us find values to try.
Though sometimes we can try some basic values first, as we may get lucky and find a zero/root.
A good value to try initially is usually 0 or 1.
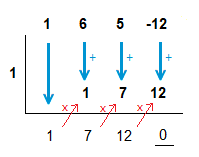
Factoring further.
Success on this occasion, we have quickly found another zero/root.
It doesn’t always work out like this, but it’s nice when it does.
Now we can factor fully and solve.
(x^2 + 7x + 12)(x \space {\text{–}} \space 1)(x + 2)
(x \space {\text{–}} \space \space \space \space )(x \space {\text{–}} \space \space \space \space )(x \space {\text{–}} \space 1)(x + 2) => (x + 3)(x + 4)(x \space {\text{–}} \space 1)(x + 2)
x + 3 = 0 \space \space {\scriptsize{=>}} \space \space x = {\text{-}}3 \space \space \space , \space \space \space x + 4 = 0 \space \space {\scriptsize{=>}} \space \space x = {\text{-}}4
x \space {\text{–}} \space 1 = 0 \space \space {\scriptsize{=>}} \space \space x = 1 \space \space \space , \space \space \space x + 2 = 0 \space \space {\scriptsize{=>}} \space \space x = {\text{-}}2
The solutions of f(x) = x^4 + 8x^3 + 17x^2 \space {\text{–}} \space 2x \space {\text{–}} \space 24 are x = {\text{-}}4 \space , \space {\text{-}}3 \space , \space {\text{-}}2 \space , \space 1.