A polynomial expression in one variable is of the following standard form.
a_{n}x^n \space + \space a_{n{\text{--}}1}x^{n{\text{--}}1} \space + \space ...... \space + \space a_{2}x^2 \space + \space a_{1}x \space + \space a_{0} ( where a_{n} \space {\cancel{=}} \space 0 )
When we encounter examples of polynomial expressions, the terms involved can be constants, or variables with a positive whole number exponent.
Parts of a Polynomial
We can observe a standard polynomial expression to identify the different parts that make up the polynomial.
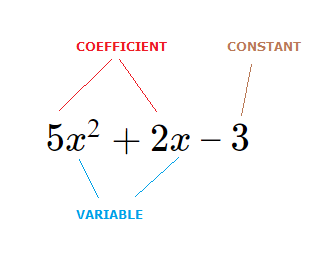
Variable:
x is a ‘variable’, which represents a numerical value that can change.A range of letters or symbols can be used for variables, but most commonly seen is the letter x.
There can also be more than one variable present in a polynomial.
A variable in a polynomial must have an exponent that is non negative and a whole number.
Terms such as x^{\tt{{\text{-}}3}}, \sqrt{x} and x^{1/4} are not allowed in polynomials.
Coefficient:
5 and 2 are coefficients.Numbers that exist alongside and multiply a variable.
Unlike variables, coefficients are allowed to have fractional exponents, and can be fractions also.
Coefficients like \sqrt{5} and \frac{1}{2} are perfectly fine.
Constant:
3 is a constant, and unlike a variable is always the same value in the polynomial.Degree of a Polynomial
The degree of a polynomial in one variable, is the largest exponent of that variable that is present.2x^{\tt{3}} + 4x \space {\text{--}} \space 5 is a polynomial expression of degree “3“.
x^{\tt{2}} \space {\text{--}} \space 3x + 4 is a polynomial expression of degree “2“.
The degree of a polynomial is an indication of how many roots/solutions the polynomial has.
A polynomial of degree “2” has at most 2 solutions.
A polynomial of degree “3” has at most 3 solutions, and so on.
Polynomial Names:
Polynomials can have specific names depending on the degree.– A linear polynomial is of degree 1, for example x + 6.
– A quadratic polynomial is of degree 2, for example x^{\tt{2}} + 2x + 3.
– A cubic polynomial is of degree 3, for example x^{\tt{3}} \space {\text{--}} \space x + 7.
There are names for larger degree polynomials also but the three listed above are usually the most common to encounter.
A constant is also a type of polynomial, if you have just a number such as 4,
this is technically a polynomial of degree “1”.
There doesn’t always need to be a variable present.
It should also be mentioned that degree can sometimes be referred to as ‘order’.
Examples of Polynomial Expressions,
Equations and Functions
Polynomial Equations:
When a polynomial is presented in the form x^{\tt{2}} + 4x + 2,it is a polynomial expression.
But we can also write as a polynomial equation or function.
A polynomial equation is when a polynomial is set equal to a certain value, even zero.
x^{\tt{2}} + 4x + 2 = 0 and x^{\tt{2}} + 4x + 2 = 9 are both examples of a polynomial equation.
We can solve many polynomial equations and find the roots/solutions.
We see how this can be done in further sections, but as mentioned earlier in this page, a polynomial equation will not have more solutions than what the degree of the equation is.
So x^{\tt{2}} + 4x + 2 = 0 and x^{\tt{2}} + 4x + 2 = 9 would both have at most 2 solutions.
Polynomial Functions:
A polynomial can presented and written as a polynomial function.
Where we could solve for a range of values that could be input into the polynomial.
f(x) = x^{\tt{2}} + 4x + 2 and f(x) = 4x^{\tt{3}} \space {\text{--}} \space x^2 + 4x + 2
are examples of polynomial functions.