In the Algebra 1 section it was shown how to work out the discriminant of a quadratic equation, and how it can be useful to do so.
For ax^2 + bx + c \space \space \space , \space \space \space \triangle = b^2 \space {\text{–}} \space 4acThe discriminant \triangle could be positive, negative or zero.
With the result telling you about the type of roots/zeros the quadratic had.
b^2 \space {\text{–}} \space 4ac \space > \space 0 , real distinct roots
b^2 \space {\text{–}} \space 4ac \space = \space 0 , real equal roots
b^2 \space {\text{–}} \space 4ac \space < \space 0 , complex roots
Things work the same way with the discriminant of a cubic equation, but it takes a bit more work than the quadratic case.
Discriminant of a Cubic Formula
For a standard cubic equation, ax^3 + bx^2 + cx + d = 0.
The discriminant is given by the following.
\space {\triangle}_3 \space = \space b^{\tt{2}}c^{\tt{2}} \space {\text{–}} \space 4ac^{\tt{3}} \space {\text{–}} \space 4b^{\tt{3}}d \space {\text{–}} \space 27a^{\tt{2}}b^{\tt{2}} + 18abcd
A cubic equation of degree 3 will have at most 3 roots/solutions, which will be one of the following.
If {\triangle}_3 > 0, 3 distinct real roots/zeros.
If {\triangle}_3 = 0, 3 real roots/zeros, of which 2 are equal.
If {\triangle}_3 < 0, 1 real root/zero, and 2 complex roots which are a conjugate pair.
Discriminant of a Cubic Equation
Examples
(1.1)
Determine the nature of the zeros/roots of the cubic equation, x^3 + 4x^2 + 2x \space {\text{–}} \space 1.
Solution
a = 1 \space , \space b = 4 \space , \space c = 2 \space , \space d = {\text{-}}1
Using the formula.
{\triangle}_3 \space = \space b^{\tt{2}}c^{\tt{2}} \space {\text{–}} \space 4ac^{\tt{3}} \space {\text{–}} \space 4b^{\tt{3}}d \space {\text{–}} \space 27a^{\tt{2}}b^{\tt{2}} + 18abcd
{\triangle}_3 \space = \space (4)^{\tt{2}}(2)^{\tt{2}} \space {\text{–}} \space 4(1)(2)^{\tt{3}} \space {\text{–}} \space 4(4)^{\tt{3}}({\text{-}}1) \space {\text{–}} \space 27(1)^{\tt{2}}(4)^{\tt{2}} + 18(1)(4)(2)({\text{-}}1)
= \space 64 \space {\text{–}} \space 32 + 256 \space {\text{–}} \space 27 \space {\text{–}} \space 154 \space = \space 107
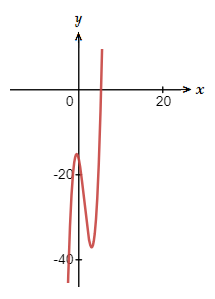
The graph of this polynomial is shown below, and as expected from the discriminant result, there are 3 distinct real roots/zeros.
(1.2)
Determine the nature of the zeros/roots of the cubic equation, x^3 + x^2 \space {\text{–}} \space 8x \space {\text{–}} \space 12.
Solution
a = 1 \space , \space b = 1 \space , \space c = {\text{-}}8 \space , \space d = {\text{-}}12
{\triangle}_3 \space = \space b^{\tt{2}}c^{\tt{2}} \space {\text{–}} \space 4ac^{\tt{3}} \space {\text{–}} \space 4b^{\tt{3}}d \space {\text{–}} \space 27a^{\tt{2}}b^{\tt{2}} + 18abcd
{\triangle}_3 \space = \space (1)^{\tt{2}}({\text{-}}8)^{\tt{2}} \space {\text{–}} \space 4(1)({\text{-}}8)^{\tt{3}} \space {\text{–}} \space 4(1)^{\tt{3}}({\text{-}}12)
{\text{–}} \space 27(1)^{\tt{2}}({\text{-}}12)^{\tt{2}} + 18(1)(1)({\text{-}}8)({\text{-}}12)
= \space 64 + 2048 + 48 \space {\text{–}} \space 3888 + 1728 \space = \space 0
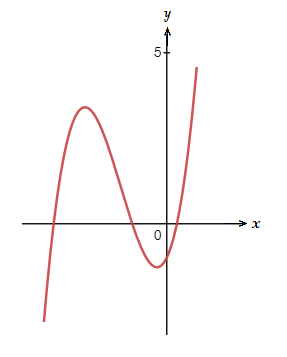
As we see in the polynomials graph below, there are 3 real roots, of which 2 are equal in the negative direction of the x-axis.
(1.3)
Determine the nature of the zeros/roots of the cubic equation, x^3 \space {\text{–}} \space 4x^2 \space {\text{–}} \space 4x \space {\text{–}} \space 16.
Solution
a = 1 \space , \space b = {\text{-}}4 \space , \space c = {\text{-}}4 \space , \space d = {\text{-}}16
{\triangle}_3 \space = \space b^{\tt{2}}c^{\tt{2}} \space {\text{–}} \space 4ac^{\tt{3}} \space {\text{–}} \space 4b^{\tt{3}}d \space {\text{–}} \space 27a^{\tt{2}}b^{\tt{2}} + 18abcd
{\triangle}_3 \space = \space ({\text{-}}4)^{\tt{2}}({\text{-}}4)^{\tt{2}} \space {\text{–}} \space 4(1)({\text{-}}4)^{\tt{3}} \space {\text{–}} \space 4({\text{-}}4)^{\tt{3}}({\text{-}}16)
{\text{–}} \space 27(1)^{\tt{2}}({\text{-}}16)^{\tt{2}} + 18(1)({\text{-}}4)({\text{-}}4)({\text{-}}16)
= \space 256 + 256 \space {\text{–}} \space 4096 \space {\text{–}} \space 6912 \space {\text{–}} \space 4608 \space = \space {\text{-}}15104
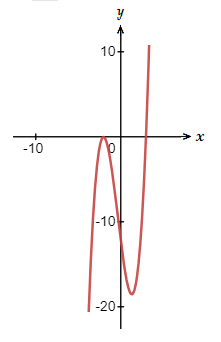
A negative discriminant value tells us that there is just one real root on the x-axis.