On the complex numbers examples/introduction page, we saw how complex numbers can be multiplied in Cartesian form.
They can also be multiplied in Polar Form.
There is a very handy theorem called De Moivre theorem, courtesy of French Mathematician Abraham De Moivre. Which can help specifically with powers of complex numbers in Polar Form.
This will be covered further on in this section, but we’ll look at some simpler examples of multiplication first.
Examples
(1.1)
Multiplying by a positive whole number.
With a ∈ \natnums,
if z = r(cosθ + isinθ), then
az = ar(cosθ + isinθ).
What this does in an Argand Diagram is stretch the vector z, by a factor of a.
So for z = 2√2(cos(\bf{\frac{\pi}{4}}) + isin(\bf{\frac{\pi}{4}})).
2z = 4√2(cos(\bf{\frac{\pi}{4}}) + isin(\bf{\frac{\pi}{4}}))
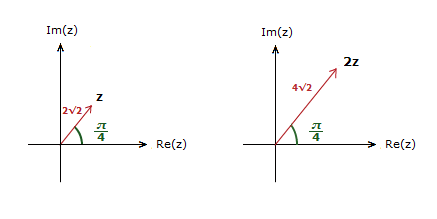
(1.2)
Multiplying by i.
Something interesting actually happens when we multiply a complex number by i.
For example with 2 + 3i:
i × (2 + 3i) = 2i + 3i2 = 2i − 3
Which plotted as a vector results in a rotation of \bf{\frac{\pi}{2}}, or 90°, anti clockwise from the original vector.
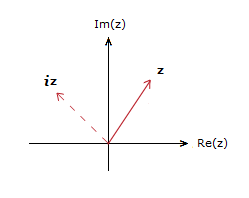
This actually happens each time you multiply by i.
Thus in Polar Form, the effect of multiplying by i, is to add \bf{\frac{\pi}{2}} to the argument.
If z = r(cosθ + isinθ), then
iz = r(cos(θ+\bf{\frac{\pi}{2}}) + isin(θ+\bf{\frac{\pi}{2}}).
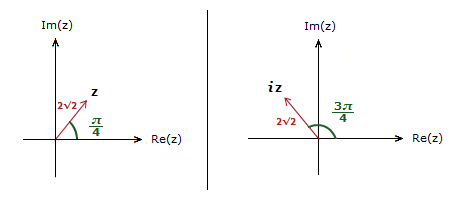
So for z = 2√2(cos(\bf{\frac{\pi}{4}}) + isin(\bf{\frac{\pi}{4}})).
iz = 2√2(cos(\bf{\frac{\pi}{4}}+\bf{\frac{\pi}{2}}) + isin(\bf{\frac{\pi}{4}}+\bf{\frac{\pi}{2}}))
= 2√2(cos(\bf{\frac{3\pi}{4}}) + isin(\bf{\frac{3\pi}{4}}))
(1.3)
Multiplying Polar Form numbers together.
If z = r(cosθ + isinθ),
and w = s(cosφ + isinφ).
Then zw = rs(cos(θ+φ) + isin(θ+φ)).
For z = 2(cos(\bf{\frac{\pi}{3}}) + isin(\bf{\frac{\pi}{3}})),
and w = 2(cos(-\bf{\frac{\pi}{6}}) + isin(-\bf{\frac{\pi}{6}})).
zw = 2x2(cos(\bf{\frac{\pi}{3}} − \bf{\frac{\pi}{6}}) + isin(\bf{\frac{\pi}{3}} − \bf{\frac{\pi}{6}}))
= 4(cos(\bf{\frac{\pi}{6}}) + isin(\bf{\frac{\pi}{6}}))
De Moivre Theorem
If we consider example (1.3) from above again.
But now instead of multiplying 2 different complex numbers together, multiply the same one with itself.
So, z = r(cosθ + isinθ), with z = r(cosθ + isinθ).
Then:
z2 = rr(cos(θ+θ) + isin(θ+θ))
= r2(cos(2θ) + isin(2θ))
So, (r(cosθ + isinθ))2 = r2(cos(2θ) + isin(2θ)).
It’s also the case that, (r(cosθ + isinθ))3 = r3(cos(3θ) + isin(3θ)).
In fact, this is the case for any integer power.
(r(cosθ + isinθ))n = rn(cos(nθ) + isin(nθ)) , n ∈ ℤ
This is De Moivre’s Theorem, and is something that can be very helpful for computing powers of complex numbers.
Examples
(2.1)
Compute (1 + i)3.
Solution
First step is to convert to Polar Form.
r = \bf{\sqrt{1^2 \space + \space 1^2}} = √2 , θ = tan-1(\bf{\frac{1}{1}}) = \bf{\frac{\pi}{4}}
z = √2(cos(\bf{\frac{\pi}{4}}) + isin(\bf{\frac{\pi}{4}}))
Now
z3 = (√2(cos(\bf{\frac{\pi}{4}}) + isin(\bf{\frac{\pi}{4}}))3
= 2√2(cos(\bf{\frac{3\pi}{4}}) + isin(\bf{\frac{3\pi}{4}}))
[ cos\bf{\frac{3\pi}{4}} = –cos\bf{\frac{\pi}{4}} = –\bf{\frac{1}{\sqrt{2}}} ] [ sin\bf{\frac{3\pi}{4}} = sin\bf{\frac{\pi}{4}} = \bf{\frac{1}{\sqrt{2}}} ]
=> z3 = 2√2(-\bf{\frac{1}{\sqrt{2}}} + i\bf{\frac{1}{\sqrt{2}}})
= –\bf{\frac{2\sqrt{2}}{\sqrt{2}}} + i\bf{\frac{2\sqrt{2}}{\sqrt{2}}} = –2 + i2
(2.2)
Compute (1 − i√3)9.
Solution
Converting to Polar Form.
r = \bf{\sqrt{1^2 \space + \space({\text{-}}\sqrt{3})^2}} = 2, θ = tan-1(\bf{\frac{{\text{-}}\sqrt{3}}{1}}) = –\bf{\frac{\pi}{3}}
z = 2(cos(-\bf{\frac{\pi}{3}}) + isin(-\bf{\frac{\pi}{3}}))
Now
z9 = (2(cos(-\bf{\frac{\pi}{3}}) + isin(-\bf{\frac{\pi}{3}})))9
= 512(cos(-\bf{\frac{9\pi}{3}}) + isin(-\bf{\frac{9\pi}{3}}))
= 512(cos(-3π) + isin(-3π))
[ cos(-3π) = -1 ] [ sin(-3π) = 0 ]
=> z9 = 512(-1 + i0)
= –512