The complex numbers section featured a page showing how complex numbers could be roots\solutions of quadratic polynomials sometimes.
We can also encounter complex roots of polynomials of higher degree than 2.
Cubic and quartic polynomial equations of degree 3 and 4 can also have complex roots to find.
The discriminant of a cubic page explained how specifically a cubic polynomial can have all real roots, or one real root and two complex roots.
Examples of such graphs shown below.
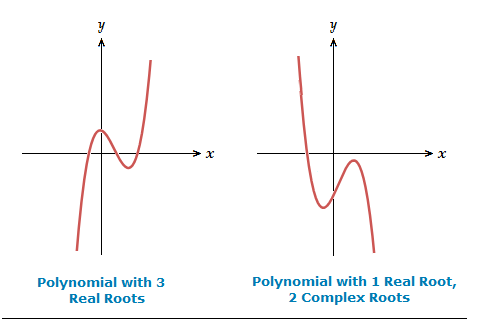
Something that can help with situations involving complex roots of polynomials is the “complex conjugate root theorem”.
Complex Conjugate Root Theorem
With a polynomial. P(x) = a_nx^n \space + \space a_{n \space {\text{–}} \space 1}x^{n \space {\text{–}} \space 1} \space + ….. + \space a_{\tt{2}}x^{\tt{2}} \space \space + a_1x \space + \space a_0
If we have a root/zero that is a complex number. P(a + ib) = 0
Then its complex conjugate is also a root. P(a \space {\text{–}} \space ib) = 0
This tells us that complex roots of polynomials are found in pairs.
So if you find one root that is complex, then you also know the value of at least one other complex zero.
Complex Roots of Polynomials
Examples
(1.1)
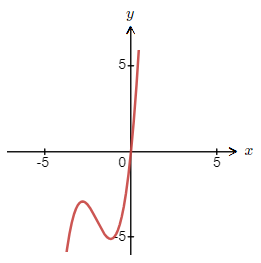
Find the roots of x^3 + 6x^2 + 10x = 0.
Solution
This polynomial can have an x factored out initially to help us along.
x^3 + 6x^2 + 10x = 0 => x(x^2 + 6x + 10) = 0
The quadratic polynomial inside the brackets can have the quadratic formula applied to solve.
ax^2 + bc + c = 0 => {\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}b \space \pm \space \sqrt{b^{2} \space – \space 4ac}}{2a}}}
x \space{\scriptsize{= \space}} {\boldsymbol{\frac{{\text{-}}6 \space \pm \space \sqrt{6^{2} \space {\text{–}} \space (4 \times 1 \times 10))}}{2 \space \times \space 1}}} {\scriptsize{=}} \space \space {\boldsymbol{\frac{{\text{-}}6 \space \pm \space \sqrt{36 \space + \space 40}}{2}}}
x \space{\scriptsize{= \space}} {\boldsymbol{\frac{{\text{-}}6 \space + \space \sqrt{{\text{-}}4}}{2}}} , {\boldsymbol{\frac{{\text{-}}6 \space {\text{–}} \space \sqrt{{\text{-}}4}}{2}}} ( \sqrt{{\text{-}}4} = \sqrt{4}\sqrt{{\text{-}}1} = 2i )
x \space{\scriptsize{= \space}} {\boldsymbol{\frac{{\text{-}}6 \space \pm \space 2i}{2}}} \space \space {\footnotesize{=}} \space \space {\small{{\text{-}}3 \pm i}}
So we have. x(x \space {\text{–}} \space ({\text{-}}3 + i))(x \space {\text{–}} \space ({\text{-}}3 \space {\text{–}} \space i)) \space = \space 0
Giving us the three roots. x \space = \space 0 \space , \space {\text{-}}3 + i \space , \space {\text{-}}3 \space {\text{–}} \space i
The graph of y = x^3 + 6x^2 + 10x is shown below.
(1.2)
Given that 2i is a root of x^3 \space {\text{–}} \space x^2 + 4x \space {\text{–}} \space 4 = 0.
Find the other roots.
Solution
As we know that 2i is a root, by the complex conjugate root theorem we also know that {\text{-}}2i is a root.
With the polynomial here being of degree 3, there are 3 roots in total, so we only need to find one more.
Writing the polynomial in factored form, with the unknown root. (x \space {\text{–}} \space 2i)(x + 2i)(x \space {\text{–}} \space a)
a is the 3rd root and is the value we need to find. We can start by multiplying out the complex factors.
(x \space {\text{–}} \space 2i)(x + 2i)(x \space {\text{–}} \space a)
= \space x^2 + x2i \space {\text{–}} \space x2i \space {\text{–}} \space 4i^2 (x \space {\text{–}} \space a) \space \space = \space \space x^2 +4(x \space {\text{–}} \space a)
We can label this result as a function, and can divide both sides.
f(x) \space = \space x^2 +4(x \space {\text{–}} \space a)
\frac{f(x)}{x^{\tiny{2}} + 4} \space = \space \frac{x^2 +4(x \space {\text{–}} \space a)}{x^2 + 4} => \frac{f(x)}{x^2 + 4} \space = \space (x \space {\text{–}} \space a)
Dividing the original polynomial by x^2 + 4 will give us the 3rd factor and root, we can use long division to do this.
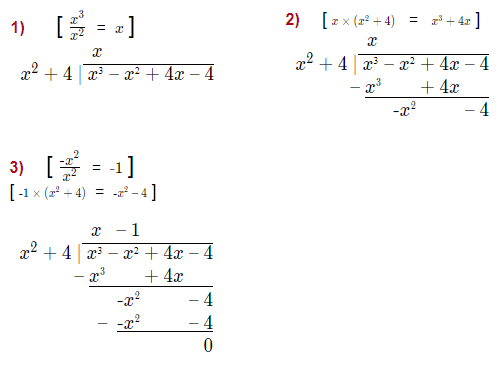
The result of the division is x \space {\text{–}} \space 1.
This is the 3rd factor, giving a 3rd root of 1.
All the solutions of x^3 \space {\text{–}} \space x^2 + 4x \space {\text{–}} \space 4= 0 are x = 1 \space , \space 2i \space , \space {\text{-}}2i.
(1.3)
Given that {\text{-}}3i is a root of x^4 \space {\text{–}} \space 4x^3 + 13x^2 \space {\text{–}} \space 36x + 36 = 0.
Find the other roots.
Solution
As we know that {\text{-}}3i is a root, by the complex conjugate root theorem we also know that 3i is a root.
With this polynomial here being of degree 4, there are 4 roots in total, so there are 2 more to find, which can be equal.
In factored form, with the unknown roots. (x \space {\text{–}} \space 3i)(x + 3i)(x \space {\text{–}} \space b)(x \space {\text{–}} \space a)
We can begin again by multiplying out the complex factors.
(x \space {\text{–}} \space 3i)(x + 3i)(x \space {\text{–}} \space b)(x \space {\text{–}} \space a)
= \space x^2 +9(x \space {\text{–}} \space b)(x \space {\text{–}} \space a)
The same approach as before can be used.
f(x) \space = \space x^2 +9(x \space {\text{–}} \space b)(x \space {\text{–}} \space a)
\frac{f(x)}{x^{\tiny{2}} + 9} \space = \space \frac{x^2 +9(x \space {\text{–}} \space b)(x \space {\text{–}} \space a)}{x^2 + 9} => \frac{f(x)}{x^2 + 9} \space = \space (x \space {\text{–}} \space b)(x \space {\text{–}} \space a)

The result of the division is x^2 \space {\text{–}} \space 4x + 4.
A quadratic which can be factored.
x^2 \space {\text{–}} \space 4x + 4 \space = \space (x \space {\text{–}} \space 2)(x \space {\text{–}} \space 2)
Thus there is only one extra real root, x = 2.
All the solutions of x^4 \space {\text{–}} \space 4x^3 + 13x^2 \space {\text{–}} \space 36x + 36 = 0 are x = 2 \space , \space 3i \space , \space {\text{-}}3i.