The complex roots page introduced how to effectively approach working out the complex roots of a polynomial that was a cubic or a quartic equation.
This page will further demonstrate the type of examples that can be encountered involving polynomials with complex solutions, and how to solve them.
Examples
(1.1)
Verify that a = 2 + i is a solution of the polynomial equation a^3 \space {\text{–}} \space 3a^2 + a + 5 = 0.
Solution
If we remember the factor theorem.
For a polynomial f(x), when f(c) = 0.
Then (x \space {\text{–}} \space c) is a factor of f(x).
So for verification we just need to input a value into the equation and obtain a result of 0.
This is true for complex numbers as well as real numbers.
Here we will have to work out, (2 + i)^3 \space {\text{–}} \space 3(2 + i)^2 + (2 + i) + 5.
(2 + i)^2 \space = \space (2 + i)(2 + i) \space = \space 4 + 4i \space {\text{–}} \space 1
(2 + i)^3 \space = \space (2 + i)(2 + i)^2 \space = \space (2 + i)(4 + 4i \space {\text{–}} \space 1) \space\space = \space\space 2 + 11i
So:
(2 + i)^3 \space {\text{–}} \space 3(2 + i)^2 + (2 + i) + 5 \space\space = \space\space 2 + 11i \space {\text{–}} \space 12 \space {\text{–}} \space 12i + 3 + 2 + i + 5 \space = \space 0
Thus a = 2 + i is a solution.
(1.2)
Solve the equation x^3 \space {\text{–}} \space 4x^2 \space {\text{–}} \space 2x + 20 = 0 given that x = {\text{-}}2 is a root.
Solution
With this example, as we already know that -2 is a root.
We can begin with the use of synthetic division.
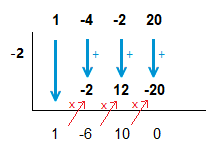
The result below now writes as x^2 \space {\text{–}} \space 6x + 10.
Giving us (x + 2)(x^2 \space {\text{–}} \space 6x + 10).
The quadratic can be factored further with the quadratic formula, giving us the other two roots of the original cubic polynomial.
Here: a = 1 \space\space , \space\space b = {\text{-}}6 \space\space , \space\space c = 10
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}b \space \pm \space \sqrt{b^{2} \space – \space 4ac}}{2a}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{6 \space \pm \space \sqrt{({\text{-}}6^{2} \space\space – \space\space (4 \times 1 \times 10)}}{2 \times 1}}} = {\boldsymbol{\frac{6 \space \pm \space \sqrt{36 \space\space {\text{–}} \space\space 40}}{2}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{6 \space \pm \space \sqrt{{\text{-}}4}}{2}}} = {\boldsymbol{\frac{6 \space \pm \space \sqrt{4 \space \times \space {\text{-}}1}}{2}}} = {\boldsymbol{\frac{6 \space \pm \space \sqrt{4}\sqrt{{\text{-}}1}}{2}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{6 \space \pm \space 2i}{2}}} \space {\scriptsize{\space = \space}} \space {\boldsymbol{\frac{6}{2} {\scriptsize\pm} \frac{2i}{2}}} \space {\scriptsize{\space = \space}} \space {\footnotesize{\boldsymbol{3 \pm i}}}
Thus, x = {\text{-}}2 \space , \space 3 + i \space , \space 3 \space {\text{–}} \space i.
Complex Roots of a Polynomial,
Further Examples
(2.1)
If x_{\tiny{1}} = 1 and x_{\tiny{2}} = 3 + 2i are solutions to x^3 + bx^2 + cx + d = 0.
Find the values of b, c and d.
Solution
As complex roots come in conjugate pairs, we know that the value of the 3rd solution is x_{\tiny{3}} = 3 \space {\text{–}} \space 2i.
So the cubic polynomial in factored form is, (x \space {\text{–}} \space 1)(x \space {\text{–}} \space (3 + 2i))(x \space {\text{–}} \space (3 \space {\text{–}} \space 2i)).
Multiplying out and expanding this factored form will give us the original polynomial with all the correct values of the coefficients b, c and d.
(x \space {\text{–}} \space (3 + 2i))(x \space {\text{–}} \space (3 \space {\text{–}} \space 2i)) \space\space = \space\space x^2 \space {\text{–}} \space 3x + 2ix \space {\text{–}} \space 3x \space {\text{–}} \space 2ix + 9 + 6i \space {\text{–}} \space 6i \space {\text{–}} \space 4i^2
= \space x^2 \space {\text{–}} \space 6x + 13
Now:
(x \space {\text{–}} \space 1)(x^2 \space {\text{–}} \space 6x + 13) \space\space = \space\space x^3 \space{\text{–}} \space 6x^2 +13x \space {\text{–}} \space x^2 + 6x \space {\text{–}} \space 13 \space\space = \space\space x^3 \space {\text{–}} \space 7x^2 + 19x \space {\text{–}} \space 13
b = {\text{-}}7 \space , \space c = 19 \space , \space d = {\text{-}}13
(2.2)
If x_{\tiny{1}} = 3i and x_{\tiny{2}} = 1 \space {\text{–}} \space i,
are complex roots of a polynomial x^4 + bx^3 + cx^2 + dx + e = 0.
Find the values of b, c, d and e.
Solution
Like in example (2.1), the two roots already given also tell us the value of the remaining roots.
x_{\tiny{1}} = 3i , x_{\tiny{2}} = 1 \space {\text{–}} \space i , x_{\tiny{3}} = {\text{-}}3i , x_{\tiny{4}} = 1 + i
In factored form, (x \space {\text{–}} \space 3i)(x + 3i)(x \space {\text{–}} \space (1 + i))(x \space {\text{–}} \space (1 \space {\text{–}} \space i)).
We can expand both pairs of roots separately, then use long multiplication to get the original quartic polynomial.
(x \space {\text{–}} \space 3i)(x + 3i) \space\space = \space\space x^2 + 9
(x \space {\text{–}} \space (1 + i))(x \space {\text{–}} \space (1 \space {\text{–}} \space i)) \space\space = \space\space x^2 \space {\text{–}} \space 2x + 2
Now:
(x^2 + 9) \times (x^2 \space {\text{–}} \space 2x + 2)
\begin{array}{r} \space\space\space\space x^{\tt{2}} \space {\text{–}} \space\space 2x + \space 2 \space\\ \times \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space x^{\tt{2}} + \space\space 0 \space + \space 9 \space\\ \hline \space 9x^{\tiny{\tt{2}}} \space {\text{–}} 18x + 18\\ x^{\tt{4}} \space {\text{–}} \space 2x^{\tt{3}} + 2x^{\tiny{\tt{2}}} \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space \\ \end{array}
=> \begin{array}{r} \space 9x^{\tiny{\tt{2}}} \space\space {\text{–}} \space 18x+ 18\\ {\color{blue}+} \space\space\space\space x^{\tt{4}} \space {\text{–}} \space 2x^{\tt{3}} + \space 2x^{\tiny{\tt{2}}} \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space \\ \hline x^{\tiny{4}} \space {\text{–}} \space 2x^{\tiny{3}} + 11x^{\tiny{\tt{2}}} \space {\text{–}} \space 18x + 18\\ \end{array}
So we get. x^4 \space {\text{–}} \space 2x^3 + 11x^2 \space {\text{–}} \space 18x + 18
Which gives us, b = {\text{-}}2 \space\space , \space\space c = 11 \space\space , \space\space d = {\text{-}}18 \space\space , \space\space e = 18.