On the Argand Diagram page. We showed how a complex number can be drawn as a vector, and expressed in Cartesian Form as well as also in polar form of complex numbers.
CARTESIAN FORM: z = a + bi
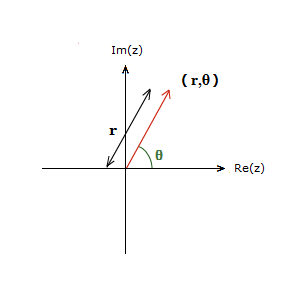
POLAR FORM: z = r(cosθ + isinθ)
Where r is the modulus, the length of the vector. r = \bf{\sqrt{a^2 \space + \space b^2}}
And θ is the argument Arg(z). The angle the vector makes with the positive direction of the Real axis.
Also shown, was how there is a need at times, to be careful when establishing the value of the argument θ.
– If a > 0, b > 0, θ = tan-1(\bf{\frac{b}{a}})
– If a > 0, b < 0, θ = tan-1(\bf{\frac{b}{a}})
– If a < 0, b > 0, θ = π + tan-1(\bf{\frac{b}{a}})
– If a < 0, b < 0, θ = –π + tan-1(\bf{\frac{b}{a}})
It’s important to be comfortable converting between the 2 complex number forms of polar and cartesian.
Polar Form of Complex Numbers,
Convert to Cartesian Form
First we’ll again look at one of the complex number examples from the Argand Diagram page, z = 1 + i√3.
The vector for this complex number is nicely placed in the 1st quadrant.
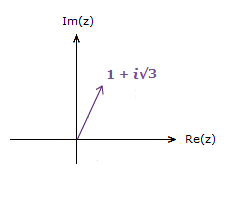
Converting to Polar Form we have:
r = \bf{\sqrt{1^2 \space + \space ({\sqrt{3}})^2}} = 2 , θ = tan-1(\bf{\frac{\sqrt{3}}{1}}) = \bf{\frac{\pi}{3}}
z = 2(cos(\bf{\frac{\pi}{3}}) + isin(\bf{\frac{\pi}{3}}))
Expanding the Polar Form:
Now this Polar Form can be expanded on slightly.The angle θ, that the vector makes with the Real axis, is called the argument, denoted Arg(z).
With the complex number above we established that it was \bf{\frac{\pi}{3}}.
But \bf{\frac{\pi}{3}} could in fact be replaced by \bf{\frac{\pi}{3}} + 2πk.
Where k is an integer. k ∈ Z
k = 0, +1, + 2, …..
This is because 2π is a full rotation on an Argand Diagram.
Taking you back to the same physical position you started from, the vector in this case.
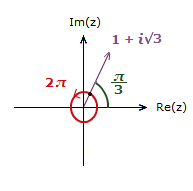
You can travel round the axis by 2π any number of times, in either direction.
So with \bf{\frac{\pi}{3}} + 2π = \bf{\frac{7\pi}{3}} and \bf{\frac{\pi}{3}} − 2π = –\bf{\frac{5\pi}{3}}.
The Polar Form of 1 + i√3 can also be:
z = 2(cos(\bf{\frac{7\pi}{3}}) + isin(\bf{\frac{7\pi}{3}}))
z = 2(cos(-\bf{\frac{5\pi}{3}}) + isin(-\bf{\frac{5\pi}{3}}))
But the original value of θ, in this case \bf{\frac{\pi}{3}}.
This is called the “principal value” of the argument Arg(z).
It is the unique value of the argument, that lies in the range, –π < Arg(z) < pi;.
As \bf{\frac{\pi}{3}} does above.
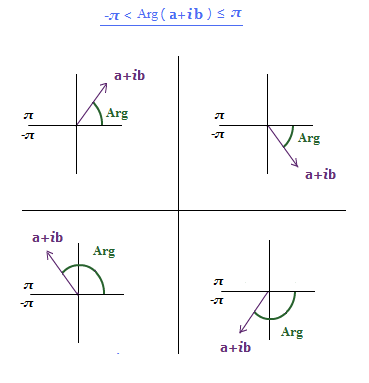
The range includes π, but not –π, so the argument of a negative real number has a principal value of π.
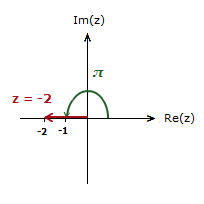
Examples
(1.1)
Convert the complex number z = 2 + i2
into Polar Form.
Solution
r = \bf{\sqrt{2^2 \space + \space 2^2}} = √8 = 2√2
a > 0 , b > 0 => θ = tan-1(\bf{\frac{2}{2}}) = \bf{\frac{\pi}{4}}
z = 2√2(cos(\bf{\frac{\pi}{4}}) + isin(\bf{\frac{\pi}{4}}))
(1.2)
Convert the complex number z = –1 + i4
into Polar Form.
Solution
r = \bf{\sqrt{({\text{-}}1)^2 \space + \space 4^2}} = √17
a < 0 , b > 0 => θ = π + tan-1(\bf{\frac{4}{{\text{-}}1}}) = 1.816 Radians
z = √17(cos(1.816) + isin(1.816))
(1.3)
Convert the complex number z = i5
into Polar Form.
Solution
r = \bf{\sqrt{0^2 \space + \space 5^2}} = 5
a = 0 , b > 0 => θ = \bf{\frac{\pi}{2}}
z = 5(cos(\bf{\frac{\pi}{2}}) + isin(\bf{\frac{\pi}{2}}))
(1.4)
Write down the Polar Form of z = –4.
Solution
r = \bf{\sqrt{({\text{-}}4)^2 \space + \space 0^2}} = 4
As z is a negative real number. The argument θ = π.
z = 4(cos(
If z = 4, the Argument would be 0.
As no angle is being made with the positive direction of the Real axis.
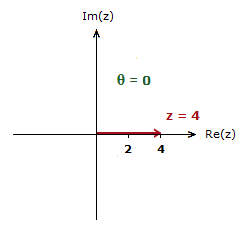
Following on from the examples shown on this page, the complex number cartesian form page shows how to convert from polar to cartesian form.
Along with introducing the exponential form of a complex number.