What are Complex Numbers?
Complex Numbers Examples

The imaginary numbers page introduced the concept of in Math, along with the part they can play in forming complex numbers.

To recap some complex numbers examples, these ‘complex numbers’ are rather special numbers in Math when they appear.
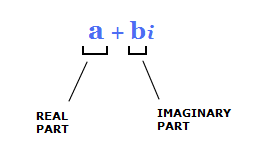
They are numbers that contain a real number part, and an imaginary number part.


To form these complex numbers, we introduce the italic letter  i  which represents  {\sqrt{{\text{-}}1}}.

Leading to a complex number having the following form.       a + bi,      a,b ∈ \Reals.

What’s special about  i,  is that when it’s squared, it gives a negative result.
This helps us deal with the roots of negative numbers when they occur.

{\sqrt{{\text{-}}x}}   =   {\sqrt{({\text{-}}1) \times x}}   =   {\sqrt{{\text{-}}1}}{\sqrt{x}}   =   i{\sqrt{x}}

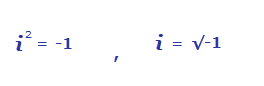
{\sqrt{{\text{{\text{-}}}}x}}   =   {\sqrt{x \times ({\text{-}}1)}}   =   {\sqrt{x}}{\sqrt{{\text{-}}1}}   =   {\sqrt{x}}i

{\sqrt{{\text{-}}16}}   =   {\sqrt{16 \times ({\text{-}}1)}}   =   {\sqrt{16}}{\sqrt{{\text{-}}1}}   =   4i



Examples    


1)    2 + i              REAL PART = 2 | IMAGINARY PART = 1

2)    3 + \bf{\frac{1}{2}}i            REAL PART = 3 | IMAGINARY PART = \bf{\frac{1}{2}}

3)    1 − 3.6i          REAL PART = 1 | IMAGINARY PART = –3.6

4)    2i                   REAL PART = 0 | IMAGINARY PART = 2

Complex Number Forms

There are also two other main ways to write a complex number in Math. A complex number can have a ‘polar form’ and an ‘exponential form’.

We go into more detail about these other forms further in the site, but to summarize.


POLAR FORM:        r(cosθ + isinθ).

Such as:  5(cos(30°) + isin(30°)).

EXPONENTIAL FORM:        re^iθ.

Such as:  4eⁱ³.

---

Complex Numbers Examples,
Non Real Roots/Solutions to Equations

One common situation where complex numbers examples crop up in Math is when we find non real roots/solutions of equations.

Below is an example of a quadratic equation solved using the quadratic formula, where the solutions turn out to non real complex solutions.

Example    


(1.1) 

Solve    2x² − 2x + 3  =  0

Solution   

Quadratic equation standard form is:
ax² + bx + c  =  0.

QUADRATIC FORMULA:     x  =  \bf{\frac{{\text{-}}b \space \pm \space {\sqrt{b^2 \space{\text{--}}\space 4ac}}}{2a}}

Here   a = 2,   b = –2,   c = 3.


x  =  \bf{\frac{{\text{-}}({\text{-}}2) \space \pm \space {\sqrt{({\text{-}}2)^2 \space{\text{--}}\space (4\times2\times3)}}}{2\times2}}    =    \bf{\frac{2 \space \pm \space {\sqrt{4 \space{\text{--}}\space 24}}}{4}}


    =    \bf{\frac{2 \space \pm \space {\sqrt{{\text{-}}20}}}{4}}    =    \bf{\frac{2 \space \pm \space {\sqrt{4}}{\sqrt{{\text{-}}5}}}{4}}    =    \bf{\frac{2 \space \pm \space 2{\sqrt{{\text{-}}5}}}{4}}

    =    \bf{\frac{1 \space \pm \space {\sqrt{{\text{-}}5}}}{2}}

( \bf{\sqrt{{\text{-}}5}}   =   \bf{\sqrt{5\times{\text{-}}1}}   =   \bf{\sqrt{{\text{-}}5}}\bf{\sqrt{1}}   =   \bf{\sqrt{5}}i )


x   =   \bf{\frac{1 \space \pm \space {\sqrt{5}}i}{2}}

    =   \bf{\frac{1 \space + \space {\sqrt{5}}i}{2}}   ,   \bf{\frac{1 \space {\text{--}} \space {\sqrt{5}}i}{2}}

Following on from this complex numbers examples page, the inverse of complex numbers page introduces the inverse and conjugate of a complex number, as well as some examples of arithmetic with complex numbers.

Arithmetic with complex numbers isn’t terribly difficult, but you do have to pay attention to the separate real and imaginary parts of the complex numbers involved.

1. Home
 ›
2. Algebra 2
› Complex Number Intro

---

Return to TOP of page