An Equilateral Triangle is a triangle where all of the sides are of the same length.
As long as we know the length of a side, the area of an equilateral triangle can be established with a standard formula.
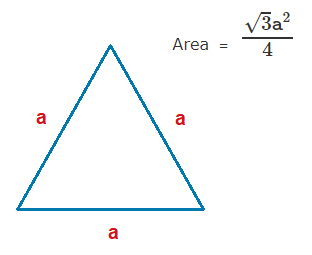
So how do we arrive at this formula?
Derive Area of an Equilateral Triangle Formula
An equilateral triangle such as the one seen above, can be split into 2 sections, with a straight line drawn from the top corner.
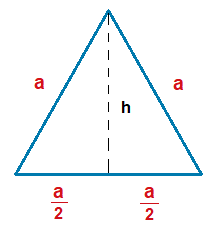
h = height
The lowest side of the triangle, the base, is also split by the dotted straight line.
Thus the length of each side of the triangle base on the left and right of the dotted line is, \bf{\frac{a}{2}}.
Equilateral Triangle as 2 Right Angle Triangles
Another way we could look at this equilateral triangle, is 2 identical right angle triangles placed together.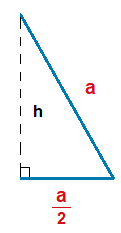
The height of one of the right angle triangles is the same as the height of the equilateral triangle.
We can work out h using Pythagoras.
h2 = a2 − (\bf\frac{a}{2})2 = a2 − \bf\frac{a^2}{4}
( a2 can be re-written as \frac{4a^2}{4}. This doesn’t change the value of the overall term a2. )
So we can have.
h2 = \bf\frac{4a^2}{4} − \bf\frac{a^2}{4} = \bf\frac{3a^2}{4}
h = \bf\sqrt{\frac{3a^2}{4}} = \bf\frac{\sqrt{3a^2}}{\sqrt{4}} = \bf\frac{\sqrt{3}\sqrt{a^2}}{\sqrt{4}} = \bf\frac{\sqrt{3}a}{2}
So the HEIGHT of the whole equilateral triangle is, \frac{\sqrt{3}a}{2}.
Formula for Area of Equilateral Triangle
The standard formula for the area of a triangle is \bf\frac{1}{2} × BASE × HEIGHT:So from what we know, for the whole equilateral triangle area.
Area = \bf\frac{1}{2} × a × \bf\frac{\sqrt{3}a}{2} = \bf\frac{1}{2} × \bf\frac{\sqrt{3}a^2}{2} = \bf\frac{\sqrt{3}a^{2}}{4}
Thus we can establish a value for the area of an equilateral triangle if we know the side length a.
Area of Equilateral Triangle Examples
(1.1)
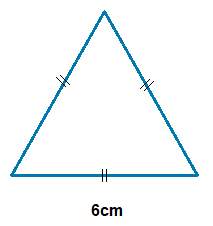
Area = \bf\frac{\sqrt{3}(6)^2}{4} = \bf\frac{\sqrt{3} \space \times \space 36}{4} = 15.59cm2
(1.2)
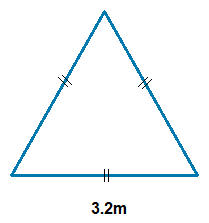
Area = \bf\frac{\sqrt{3}(3.2)^2}{4} = \bf\frac{\sqrt{3} \space \times \space 10.24}{4} = 4.43m2
(1.3)
A result of deriving the area of an equilateral triangle formula, was also obtaining a formula for the height.
h = \bf\frac{\sqrt{3}a}{2}
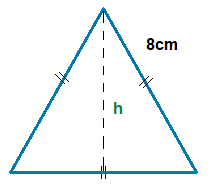
The height h of this equilateral triangle is:
h = \bf\frac{\sqrt{3} \space \times \space (8)}{2} = 6.93cm