Here we will observe how to establish the area of a rectangle and a square, and look at the area of a square formula and a rectangle making use of the diagonal length.
Area of a Rectangle or Square
The rectangle and the square are two of the most basic standard shapes in Geometry.Establishing the area of a rectangle or a square turns out to be relatively straightforward when we know the length of the sides.
Square:
A square has a width and a height that are of the same length.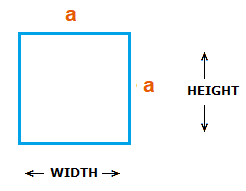
Area = WIDTH × HEIGHT
=> a × a or a2 This is the simplest area of a square formula.
Rectangle:
Now for a standard rectangle.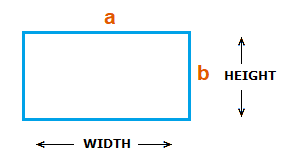
Area = WIDTH × HEIGHT
=> a × b
The differing values in the height and width in a rectangle result in the different labels.
But overall the area sum to perform is the same.
Examples
(1.1)
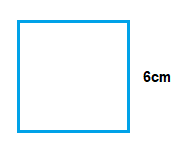
Area = 6cm × 6cm = 36cm2
(1.2)
What is the area of the following tennis court?
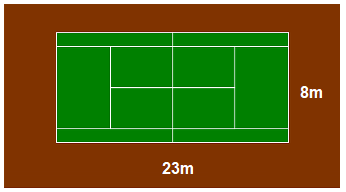
Solution
Area = WIDTH × HEIGHT
= 23m × 8m = 184m2
(1.3)
If the area of a square is 25cm2.
What length are the sides of the square?
Solution
b2 = 25cm2
b = √25 = 5
Each side of the square is 5cm in length.
(1.4)

If the area of the rectangle above is 32cm2.
What length is the width of the rectangle?
Solution
4 × w = 32 ( ÷ 4 )
w = \bf{\frac{\tt{32}}{\tt{4}}} => w = 8
The width of the shown rectangle is 8m.
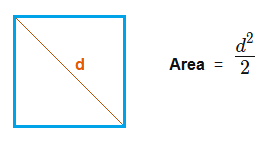
Area of a Square Formula,
Area of a Rectangle using Diagonal
There is also an alternative way to establish the area of a square, provided you know the value of the length of the diagonal.
Example
(2.1)
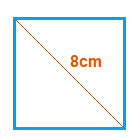
Area = \frac{8^2}{2} = \frac{64}{2} = 32
Area = 32cm2
(2.2)
When we know the width/length of a rectangle (l), and the value of the diagonal (d).
There following formula can be used.
Area = l \sqrt{d^2 \space {\text{--}} \space l^2}
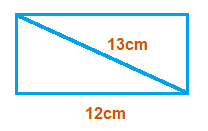
For the rectangle above.
Area = 12 \times \sqrt{13^2 \space {\text{--}} \space 12^2} = 12 \times \sqrt{25} = 12 \times 5 = 60
Area = 60cm2