Although a Hexagon as a shape has one more side/edge than a 5 sided Pentagon.
Attempting to calculate the area of a regular Hexagon with 6 sides is generally simpler to establish the area of.
Derive Area of a Hexagon Formula
We can look at a regular Hexagon shape with 6 sides, of which all are the same length.
Such a regular Hexagon like this can be divided into 6 equilateral triangles, by drawing straight lines from each corner of the Hexagon to the central point.
The triangles will all be of equal size.
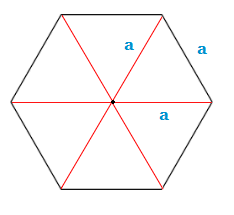
In order to calculate the area of the Hexagon in total, we would need to work out the area of one of the inner triangles, and then multiply this value by 6.
Inner Triangle Area:
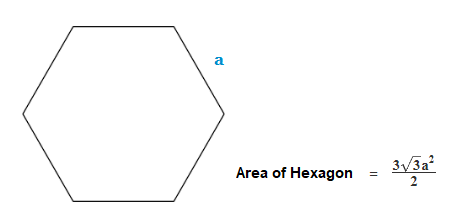
As long as we know the size of a side length of a regular Hexagon a.Then the area of one of the equilateral triangles inside is given by: \frac{\sqrt3 {\tt{a}}^2}{4}
As we see, there are 6 equilateral triangles inside a regular Hexagon, so we can multiply by a triangle area by 6.
6 × \frac{\sqrt3 {\tt{a}}^2}{4} = \frac{6\sqrt3 {\tt{a}}^2}{4} = \frac{3\sqrt3 {\tt{a}}^2}{2}
The result we get is the formula for the area of a regular Hexagon, which we can use to establish the area of a regular Hexagon, provided we know the side length size.
Examples
(1.1)
Find the area of the following regular Hexagon.
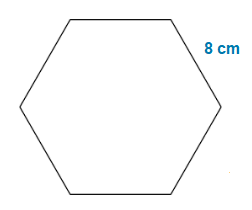
Solution
Area = \frac{3\sqrt3 (8)^2}{2} = \frac{3\sqrt3 \times 64}{2} = \frac{192\sqrt3}{2} = 166.28
Hexagon Area is 166.28cm2.
(1.2)
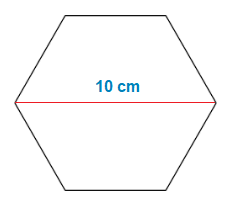
Find the area of the following Hexagon.
Solution
Here it’s the diameter of the Hexagon that we are given, rather than the side length.
But that can still be used, because the length of the diameter of a regular Hexagon, happens to be double the length of a side.
So dividing 10 by 2 will result in the value of the length of a side of the Hexagon.
10 ÷ 2 = 5
The length of a side of the Hexagon is 5cm.
Area = \frac{3\sqrt3(5)^2}{2} = \frac{3\sqrt3 \times 25}{2} = \frac{75\sqrt3}{2} = 64.95
Hexagon Area is 64.95cm2.
Area of a Hexagon Formula, Alternative
There is also slightly different area of a Hexagon formula that can be used to calculate the area of a regular Hexagon.
If we know the length of an apothem of a regular Hexagon, along with the length of all sides combined, the perimeter.
Then Hexagon Area can be found by: \frac{1}{2} × Apothem × Perimeter
The apothem in a regular Hexagon is a straight line from the central point of a side to the central point of the Hexagon itself, labelled a below.
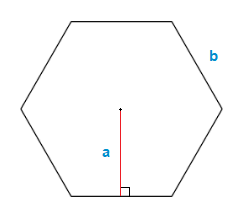
The size of an apothem line in a regular polygon such as a regular Hexagon is found by the following.
Apothem Line = \bf{\frac{b}{2 \space \times \space tan(\frac{180}{n})}}
Where n is the total number of sides, and a is the length of just one side.
Examples
(2.1)
Find the area of the following Hexagon.
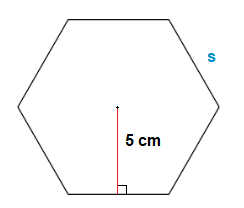
Solution
Apothem line = \bf{\frac{s}{2 \space \times \space tan(\frac{180}{n})}} ( This can help find on side length s. )
=> 5 = \bf{\frac{s}{2 \space \times \space tan(\frac{180}{6})}} = \bf{\frac{s}{2 \space \times \space tan(30)}} = \bf{\frac{s}{\frac{2}{\sqrt3}}}
=> 5 = \bf{\frac{s}{\frac{2}{\sqrt3}}}
=> 5 × \bf{\frac{2}{\sqrt3}} = s , \bf{\frac{10}{\sqrt3}} = s
s = 5.77
HEXAGON PERIMETER = 5.77 × 6 = 34.62
Hexagon Area = \frac{1}{2} × 34.62 × 5 = 86.55
The area of the Hexagon is 86.55cm2.