The 3 angles that appear inside a triangle always add up to a total of 180°.
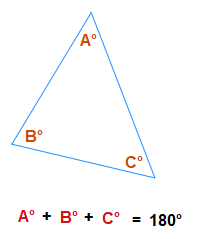
We can see this for ourselves anytime with angles in a drawn triangle.
Simply draw any standard triangle, then use an appropriate way to measure the inside angles, and the angles will add up to 180°.
Example
(1.1)
What is the size of angle b?
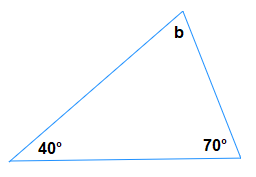
Solution
All 3 angles added together are 180°.
b = 180° − 70° − 40° = 180° − 110° = 70°When we already know the size of 2 of the angles present in a triangle, we can find the size of the third angle.
It’s also the case that the largest sized angle inside a triangle is the angle that is opposite the longest side.
With the smallest angle being the angle that is opposite the shortest side.
Triangle Exterior Angle Theorem
When it comes to exterior angles that involve triangles specifically.
There is an interesting theorem that is referred to as the “Exterior Angle Theorem”.
This theorem states that the exterior angle of a triangle is equal to the sum of the two opposite interior angles which are inside the triangle.
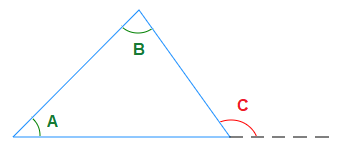
In the above triangle: Angle C = A + B
This is true because of the fact that all of the three interior angles of a triangle sum up to 180°.
Added to the fact that supplementary angles along a straight line also sum up to 180°.
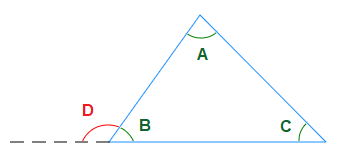
For the angles in the above triangle.
A + B + C = 180° and C + D = 180°So A + B + C = B + D.
=> A + B + C − B = D
=> A + C = D
Examples
(2.1)
What is the size of angle U ?
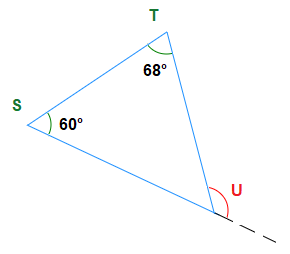
Solution
Angle U = 60° + 68° = 128°
(2.2)
What is the size of angles G and H ?
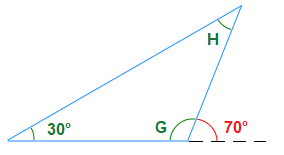
Solution
Angle H + 30° = 70°
Angle H = 70° − 30° = 40°
Angle G is Supplementary with 70°,
Angle G = 180° − 70° = 110°.