This page gives an introduction to arithmetic operations regarding both positive and negative whole numbers in Math, which are known as Integers.
Using set notation, the set of all Integers is represented by \Z.
The first type of numbers we generally encounter in Math are positive numbers.
Numbers such as 1, 42, 236.
The time does come though, when we deal with both positive and negative numbers.
Where we encounter negative numbers that have a value less than zero.
Such as -4, -25, -158.
As stated, when negative numbers are combined with positive whole numbers as a group, they make up the Integers.
……. -3 , -2 , -1 , 0 , 1 , 2 , 3 ……
Adding and Subtracting,
Positive and Negative Numbers
It’s learned very early in Math how to successfully add and subtract positive numbers in sums.
3 + 4 = 7 , 8 − 2 = 6
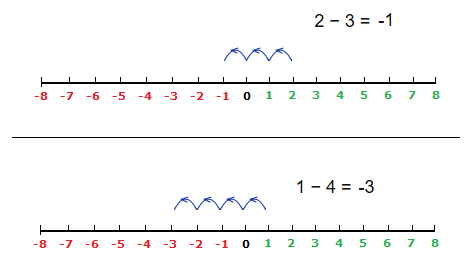
However we can also have see sums such as: 2 − 3 = -1 , 1 − 4 = -3
Sums like this can be demonstrated by showing steps taken forward or back on an appropriate number line.
Add or Subtract a Negative Number
The important thing to remember is what happens when we subtract or add a negative number.
When you subtract a negative number from another number, what you’re really doing is adding it on.
At the same time, when you add a negative number to another number, then you’re subtracting it.
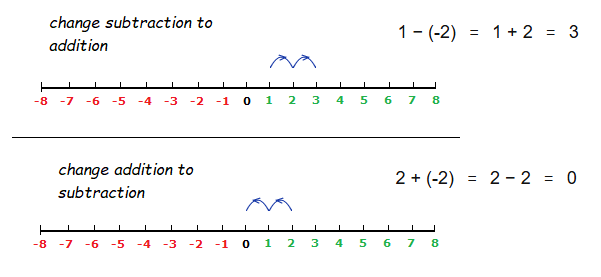
a) 1 − (-2) = 1 + 2 = 3
You are taking away 2 backwards steps, switching them to 2 forward steps.
b) 2 + (-2) = 2 − 2 = 0
You’re adding 2 backwards steps on.
We can look at a number line and see that the steps for subtraction or addition are flipped around.
Examples
(1.1) 8 + (-2) = 8 − 2 = 6
(1.2) 6 − (-5) = 6 + 5 = 11
(1.3) -3 + 1 = -2
(1.4) -3 − 1 = -4
Multiplying Positive and Negative Numbers
For the situation of multiplying positive and negative numbers. Care also has to be taken with which signs appear where.
Two numbers that are multiplied together having the same sign, result in a positive number.
+ × + = + − × − = +
But two numbers that are multiplied together with a different sign, result in a negative number.
+ × − = − − × + = −
Examples
(2.1) 10 × 3 = 30 (2.2) -3 × 2 = -6 (2.3) 2 × -6 = -12 (2.4) -6 × -4 = 24
Often we need to be a little more careful when multiplying more than only 2 numbers together, when we have both positive and negative numbers involved.
Look to move one step at a time.
(2.5) (-2) × 3 × (-4) => (-2) × 3 = -6 , -6 × (-4) = 24
(-2) × 3 × (-4) = 24
(2.6) (-2) × (-4) × (-3) => (-2) × (-4) = 8 , 8 × (-3) = -24
(-2) × (-4) × (-3) = -24
Positive and Negative Number Division
Division involving negative and positive numbers shares similarities with multiplication.
Like in the case of multiplication, with division we need to pay attention to the position of any − sign.
If both numbers in a division have the same sign, the answer is POSITIVE.
\tt{\frac{\color{blue}+ve}{\color{blue}+ve}} = +VE \tt{\frac{\color{darkred}-ve}{\color{darkred}-ve}} = +VE
If the numbers in a division have different signs, the answer is NEGATIVE.
\tt{\frac{\color{blue}+ve}{\color{darkred}-ve}} = −VE \tt{\frac{\color{darkred}-ve}{\color{blue}+ve}} = −VE
Examples
(3.1)
\frac{32}{4} = 8
\frac{32}{4} = 8
(3.2)
\frac{{\text{-}}24}{6} = -4
\frac{{\text{-}}24}{6} = -4
(3.3)
\frac{16}{{\text{-}}8} = -2
(3.4)
\frac{20}{{\text{-}}4} = -5